2. Origami vzorové riešenie

Zadanie

A keď už budete v papiernictve kupovať plastelínu na prvú úlohu, nezabudnite na origami papier. Ideálne aby to boli štvorčeky s uhlopriečkou dĺžky \(\SI{1}{\deci\metre}\). Keď si z neho budete doma skladať lodičky, zamyslite sa pri tom nad tým, kde sa bude nachádzať ťažisko útvaru, ktorý vznikne, keď z rohu takéhoto štvorca odstrihneme štvorček so štvrtinovou plochou.

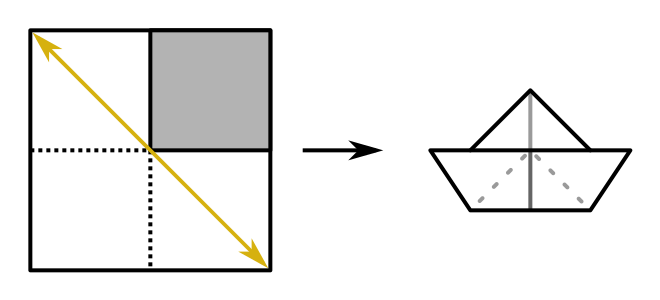
Spôsobov, ako môžeme nájsť ťažisko, je viacero. My si ukážeme dva z nich.

1. spôsob – sčítavanie ťažísk jednotlivých oblastí

Na zistenie polohy ťažiska telesa sa dá použiť spôsob, kde rozkúskujeme teleso na časti, pre ktoré polohu ťažiska určiť vieme a následne urobíme vážený priemer týchto polôh. Vážený priemer je veľmi podobný aritmetickému priemeru, ktorý sa učí v škole, avšak vo váženom priemere uvažujeme aj o „váhach“ hodnôt. Je to ten istý spôsob, ako napríklad vypočítať priemernú známku.

Každé číslo vynásobíme jeho váhou a po sčítaní vydelíme súčtom všetkých váh. Keby sme mali napríklad 5 jednotiek, 3 dvojky, 1 trojku a 2 štvorky, vážený priemer by sme vypočítali ako \[ P=\frac {5\cdot \mathbf{1} + 3\cdot \mathbf{2} +1\cdot \mathbf{3}+2\cdot \mathbf{4}}{5+3+1+2}=\frac {22}{11}=2\text{.} \]

Prv, než budeme robiť priemer, však musíme poznať hodnoty, ktoré budeme priemerovať. A teda si musíme papier rozdeliť na nejaké časti, určiť im ťažiská a následne urobiť vážený priemer \(x\)-ových a \(y\)-ových súradníc jednotlivých ťažísk. Výsledkom budú súradnice hľadaného miesta.

Rozdeliť si papier na časti a nájsť im ťažiská je v tomto prípade najľahšia časť, keďže papier možno rozdeliť na tri rovnako veľké štvorce. Nájsť ťažisko štvorca je jednoduché, keďže leží v jeho strede (resp. na prieniku jeho uhlopriečok). Ostáva nám teda zistiť súradnice stredov štvorcov. Na to potrebujeme vedieť dĺžku hrany papiera. Keďže poznáme dĺžku uhlopriečky, hranu ľahko vypočítame využitím Pytagorovej vety.

\[ \begin{aligned} a^2 + a^2 &= \SI{1}{\deci\meter}^2\text{,} \\ a &= \sqrt{\frac{1}{2}} = \frac{\sqrt{2}}{2}\text{.} \end{aligned} \]

Používať tento výraz vo výpočtoch môže byť trochu mätúce, budeme miesto neho teda používať „\(a\)“. Ak si teraz ľavý dolný roh určíme ako bod so súradnicami \([0, 0]\), ľahko vidieť, že \(x\)-ové súradnice stredov štvorcov budú \(a/4\), \(a/4\), \(a\cdot 3/4\) a \(y\)-ové súradnice budú taktiež \(a/4\), \(a/4\), \(a\cdot 3/4\).

Teraz nám už ostáva urobiť vážený priemer. Môžme si všimnúť, že všetky tri časti sú rovnako veľké a teda im všetkým môžeme prisúdiť rovnakú váhu, napr. 1¹: \[ \begin{aligned} x_T &=\frac {\frac a4+\frac a4+\frac {3\cdot a}4}{3}=\frac 5{12}\cdot a=\frac {\sqrt 2 \cdot 5}{24} \doteq \SI{0.2946}{\deci\meter}\text{,} \\ y_T &=\frac {\frac a4+\frac a4+\frac {3\cdot a}4}{3}=\frac 5{12}\cdot a=\frac {\sqrt 2 \cdot 5}{24} \doteq \SI{0.2946}{\deci\meter}\text{.} \end{aligned} \]

Teda súradnice ťažiska sú \([\SI{0.2946}{\deci\meter}, \SI{0.2946}{\deci\meter}]\).

2. spôsob – odpočítavanie stratených častí

Tento spôsob je veľmi podobný tomu prvému, ale teraz aj odpočítavame. Pri predošlom spôsobe sme akoby „sčítavali“ ťažiská nejakých pomyselných častí a hľadali k nim bod, ktorý by bol ich priemerom. Dá sa na to pozrieť aj tak, že sme akoby sčítavali tiažové sily jednotlivých týchto častí. Pri tomto druhom spôsobe uvažujeme aj o silách opačne orientovaných.

Predstavme si, že rovnako, ako v predošlom spôsobe sily sčítavame, ale ak nejakú časť nepridávame, ale odpočítavame, táto sila bude opačne orientovaná. Bude záporná. V našom prípade zo stredu štvorca ide sila \(\vec{F}\) a zo stredu chýbajúceho štvorca ide sila veľkosti \(-\vec{F}/4\). To znamená, že váha menšej časti je \(-1\) a váha väčšej \(4\).

Vo všeobecnosti platí, že ak v nejakom útvare chýba malá časť, ťažisko útvaru vieme zistiť tak, že od tohoto útvaru odpočítame túto malú časť. Avšak všetky tieto odpočítania a pričítavania počítame cez vážený priemer.

\[ \begin{aligned} x_T &= \frac {\frac a2\cdot4-\frac {3\cdot a}4\cdot 1}{4-1}\text{,} \\ y_T &= \frac {\frac a2\cdot4-\frac {3\cdot a}4\cdot 1}{4-1}\text{.} \end{aligned} \]

Tu vidíme, že nám vyšiel ten istý bod, ako v prvom spôsobe.