2. Kvíčo Držgroš vzorové riešenie

V celom vzoráku budem počítať s tým, že plocha Mesiaca, na ktorú sa pozeráme, je kruh, a nie polguľa, lebo je oveľa jednoduchšie počítať s kruhom ako s polguľou. Môžem to robiť preto, lebo povrch kruhu je \[ S_k=\pi r^2 \]

a povrch gule je \[ S_g = 4\pi r^2\text{.} \]

Mesiac vidíme iba z jednej strany, a preto maximálny pozemok, ktorý môžeme vidieť, je polovica povrchu mesiaca, teda polguľa. Povrch polgule je \[ \frac{S_g}{2} = \frac{4\pi r^2}{2} = 2\pi r^2\text{.} \]

Vidíme teda, že skutočný povrch polgule je dvakrát taký veľký, ako povrch kruhu s rovnakým polomerom. Čím menšiu plochu vezmeme z povrchu gule, tým menej sa nám na nej prejaví zakrivenie. Podobne, ako môžeme mať pocit, že Zem je plochá, lebo z nej vidíme iba príliš malý výsek. Maximálny možný rozdiel medzi povrchom kruhu a povrchom časti gule (medzi tým, keď rátame so zakrivením a keď nie) teda je, že pozemok na guli môže byť dvakrát taký veľký ako na rovine, a teda to môžeme zanedbať.

Nakreslime si teda obrázok, ako to približne vyzerá:

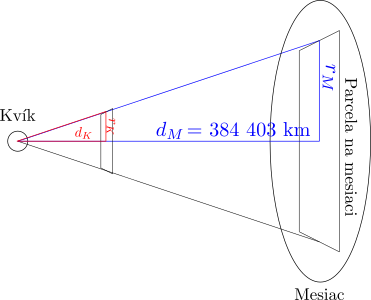
Z obrázka vidíme, že trojuholník, ktorý má strany \(r_K\) a \(d_K\) (ten menší, červený) je podobný s trojuholníkom so strany \(r_M\) a \(d_M\) (ten väčší, modrý). Vieme, že podobné trojuholníky majú strany v rovnakom pomere. Teda vieme, že \[ \frac{d_K}{d_M} = \frac{r_K}{r_M}\text{.} \]

Z tejto rovnice si vyjadríme dĺžku parcely na povrchu Mesiaca \[ r_M = \frac{d_M r_K}{d_K}\text{.} \]

Keďže parcely bývajú väčšinou štvorcové, alebo obdĺžnikové, povrch štvorcovej parcely, ktorý vidí Kvík, je \[ S_K = \left(2 r_K\right)^2 \]

a povrch „reálnej“ parcely na Mesiaci je \[ S_M = \left(2 r_M\right)^2\text{.} \]

Predtým sme si už polovicu dĺžky parcely \(r_M\) vyjadrili, a teda ho môžeme dosadiť do tejto rovnice, čím dostaneme \[ S_M = \left(2\frac{d_M r_K}{d_K}\right)^2\text{.} \]

Pomer týchto dvoch plôch si teda vieme vypočítať ako \[ k = \frac{S_M}{S_K} = \frac{(2 \frac{d_M r_K}{d_K})^2}{(2 r_K)^2} = \frac{2^2 \frac{d_M^2 r_K^2}{d_K^2}}{\frac{2^2 r_K^2}{1}} = \frac{2^2 r_K^2 d_M^2}{2^2 r_K^2 d_K^2} = \frac{d_M^2}{d_K^2}\text{.} \]

Z tohto nám teda vyplýva, že pomer plôch je rovnaký ako pomer druhých mocnín týchto dvoch vzdialeností.

Priemerná vzdialenosť Mesiaca od Zeme je \(\SI{384 403}{\kilo\meter}=\SI{384 403 000}{\meter}\). Po dosadení hodnôt teda máme: \[ k = \frac{\left(\SI{384403000}{\metre}\right)^2}{\left(\SI{0.8}{\metre}\right)^2} = \frac{\num{147765666409000000}}{\num{0.64}} = \num{230 883 853 764 062 500}\text{.} \]

Teda vidíme, že parcela na Mesiaci je \(\num{230 000 000 000 000 000}\)-krát väčšia ako parcela, ktorú vidí Kvík.