4. Napoleon EnplusPrvý vzorové riešenie

Zadanie

Ide si tak svetelný lúč priestorom, keď tu zrazu vidí pred sebou škatuľu s otvormi v dvoch susedných rohoch. Vojde dnu a zistí, že v škatuli sú zvnútra zrkadlá. Toto bude zábava, povie si lúč, a odrazí sa od steny vo vzdialenosti \(\SI{25}{\centi\metre}\) od rohu škatule. Tak sa veselo odráža od stien škatule, kým nevyletí cez dieru zase von.

Lúč by teraz rád vedel, akú dráhu prešiel, kým vyšiel von zo škatule. Škatuľa je znázornená na obrázku, jej hrana má dĺžku \(\SI{1}{\metre}\) a v rohoch oproti otvorom má malé zrkadielka zvierajúce s blízkymi stenami uhol \(\ang{135}\).

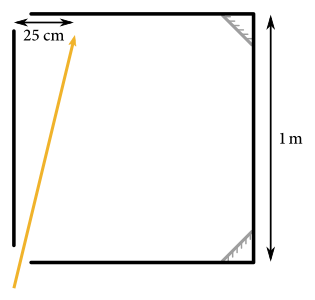
Aby sme spočítali dráhu lúča, musíme ju najskôr nájsť. Lúč na začiatku vojde do škatule presne v jej rohu a odrazí sa od náprotivnej steny vo vzdialenosti \(\SI{25}{\centi\metre}\), čiže na začiatku zviera s ľavou stenou škatule uhol \(\phi = \arctan{\frac{25}{100}}\). Tu si môžeme všimnúť, že normála steny škatule v bode, kde lúč dopadol je rovnobežná s ľavou stenou škatule a teda lúč zviera s normálou tiež uhol \(\phi\) – uhol dopadu.

Zákon odrazu nám hovorí, že uhol dopadu lúča \(\phi\) sa bude rovnať uhlu odrazu (tieto uhly meriame od normály v bode dopadu lúča). Vďaka tomu bude odrazený lúč symetrický podľa normály s odrážajúcim sa lúčom. Keďže škatula je štvorec, protilahlé steny škatule sú rovnobežné a teda lúč dopadne na protiľahlú stenu \(\SI{25}{\centi\metre}\) doprava od posledného odrazu, čiže do jej stredu, znovu s uhlom \(\phi\) a s ním sa aj odrazí. Takto sa lúč odtazí ešte raz na hornej stene a dopadne na zrkadielko v pravom dolnom rohu.

Zrkadielko je oproti stene pootočené o \(\ang{45}\) a lúč teda na neho dopadá aj sa odráža v uhle \(\psi = \ang{45} -\phi\). Tu si všimnime, že odrazený lúč zviera so spodnou stenou škatule opäť uhol \(\phi\), rovnako ako pri vstupe do škatule s jej ľavou stenou. Z toho môžeme usúdiť, že pohyb lúča počas nasledujúcich štyroch odrazov bude rovnaký ako pohyb počas prvých štyroch odrazov, len otočený okolo stredu škatule o \(\ang{90}\) proti smeru hodinových ručičiek.

Takto sa dostaneme k hornému zrkadielku, od ktorého sa lúč odráža pod uhlom \(\psi\), čiže zviera s ľavou stenou škatule opäť uhol \(\phi\), z čoho vieme odhadnúť, že lúč opäť vykoná podobnú sériu štyroch odrazov, tentokrát pootočených okolo stredu o ďaľších \(\ang{90}\), čiže \(\ang{180}\) oproti prvej sade. S tým rozdielom, že posledný odraz sa nevykoná (nie je o čo, v tomto rohu škatule je diera), ale lúč vyletí z škatule v ľavom hornom rohu.

Teraz už poznáme dráhu lúča a je ľahko vidno, že sa skladá z 12 rovnako dlhých trajektórií, rozdelených 11 odrazmi. Spočítajme si teda ešte dĺžku jednej z nich, napríklad prvej. Tá spolu s ľavou stenou škatule a prvými \(\SI{25}{\centi\metre}\) hornej steny tvorí pravouhlý trojuholík, takže ju vieme spočítať pomocou Pytagorovej vety: \[ \sqrt{\left(\SI{100}{\centi\metre}\right)^2 + \left(\SI{25}{\centi\metre}\right)^2} = 25 \SI[parse-numbers = false]{\sqrt{17}}{\centi\metre}\text{.} \]

To znamená, že celá dráha mala dĺžku \(12 \cdot 25 \SI[parse-numbers = false]{\sqrt{17}}{\centi\metre} = 300 \SI[parse-numbers = false]{\sqrt{17}}{\centi\metre}\).