4. Krtečkove pochôdzky vzorové riešenie

Zadanie

Jeden Krtko o hmotnosti \(m_2=\SI{70}{\kilo\gram}\) si povedal, že hydraulické zdviháky sú sranda, a tak raz na jeden vyliezol. Zdvihák mal dva piesty s plochami \(S_1=\SI{0.5}{\square\metre}\) a \(S_2=\SI{3}{\square\metre}\). Krtko skoro zistil, že niečo nie je v poriadku, pretože síce stál na pieste, ale piest nestál na mieste. Všimol si, že na druhom pieste si tróni závažie o hmotnosti \(m_1=\SI{113}{\kilo\gram}\), o ktoré je previazané lano prevedené cez kladku. Krtko sa chopil príležitosti aj lana a potiahol. Piesty sa zastavili. Akou silou Krtko ťahal?

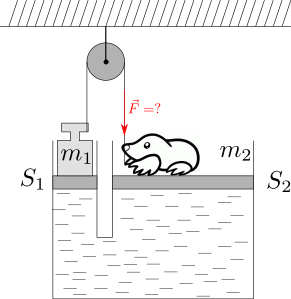
Na začiatok si vyjadríme, akou silou tlačia Krtko a závažie na piesty. Krtko a závažie pôsobia na piesty gravitačnou silou, ktorá je kolmá na piesty. Najskôr si vyjadríme silu pre Krtka \[F_{gK} = m_2g\]

a hneď aj silu pre závažie \[F_{gz} = m_1g\text{.}\]

Vieme, že Krtko ťahá za lano, ktoré je cez kladku pripevnené o závažie, takže celková sila, ktorou bude závažie tlačiť na piest, bude \(m_1 g - F\). Pretože lano ťahá závažie opačným smerom, ako gravitačná sila, závažie bude na piest pôsobiť menšou silou ako je gravitačná. Keď Krtko ťahá lano, tak sa nadľahčuje, keďže sa musí o lano zavesiť. Tým pádom bude pôsobiť menšou silou na piest, čo si vieme vyjadriť ako \(m_2 g - F\). Sila pôsobiaca na kladku musí byť z oboch strán rovnaká, preto máme \(-F\) na obidvoch stranách a nemáme tam nejaké dve odlišné sily.

Vďaka Pascalovmu zákonu vieme, že keď na kvapalinu pôsobia vonkajšie sily, tlak na kvapalinu je stále rovnaký. Tlak si taktiež vieme vyjadriť ako \(p = \frac{F}{S}\), čo v našom prípade budú nami vyjadrené sily tlačiace na piesty a plocha piestov.

Keďže je tlak v kvapaline všade rovnaký, vieme napísať rovnicu, z ktorej si následne vyjadríme \(F\). A to bude práve sila, ktorou Krtko ťahá lano. \[p = \frac{m_1g - F}{S_1} = \frac{m_2g - F}{S_2}\text{,}\]

Postupnými úpravami dostaneme \[\frac{m_1g - F}{S_1} = \frac{m_2g - F}{S_2}\text{,}\]

\[m_1gS_2 - FS_2 = m_2gS_1 - FS_1\text{,}\]

\[FS_1 - FS_2 = m_2gS_1 - m_1gS_2\text{,}\]

\[F (S_1 - S_2) = m_2gS_1 - m_1gS_2\text{,}\]

\[F = \frac{m_2gS_1 - m_1gS_2}{S_1 - S_2}\text{.}\]

Posledné, čo nám treba urobiť, je dosadiť do našej rovnice číselné hodnoty zo zadania. \[F = \frac{\SI{113}{\kilo\gram} \cdot \SI{9.8}{\metre\per\second\squared} \cdot \SI{3}{\metre\squared} - \SI{70}{\kilo\gram} \cdot \SI{9.8}{\metre\per\second\squared} \cdot \SI{0.5}{\metre\squared}}{\SI{3}{\metre\squared} - \SI{0.5}{\metre\squared}} \approx \SI{1192}{\newton}\]

Krtko teda ťahal lano silou asi \(\SI{1192}{\newton}\).