4. Mariankina zbierka vzorové riešenie

Zadanie

Marianka má veľmi rada kladky, a tak ich zopár vytiahla zo svojej zbierky a zostrojila si kladkostroj spojený s hydraulickými piestami ako je na obrázku. Hydraulické piesty mali plochy \(S\) a \(4S\). Chvíľu sa s ním hrala, čo v nej vyvolalo zopár otázok: Aké ťažké je závažie, ak ho drží silou \(\SI{1}{\newton}\)? O koľko musí potiahnuť lanko napravo, aby sa závažie pohlo nahor o \(\SI{1}{\centi\metre}\)? A koľko práce musí vykonať, aby závažie zdvihla o \(\SI{1}{\centi\metre}\)? Pomôžte Marianke a odpovedzte na jej otázky.

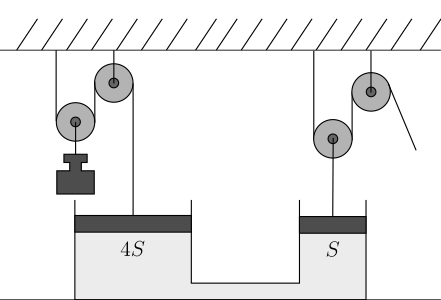
Aby sme mohli odpovedať na Mariankine otázky, potrebujeme vedieť, ako fungujú kladky a hydraulické piesty.

Pevná kladka

Pevná kladka iba mení smer pôsobenia sily. Nemení jej veľkosť.

Voľná kladka

Zato voľná kladka rozkladá silu, ktorou na ňu pôsobí závažie, na obe strany špagátu, na ktorom visí.

Na druhú stranu dráha je dvakrát dlhšia - ak chceme zdvihnúť závažie o dráhu \(l\), musíme potiahnuť až \(2l\) lana.

Hydraulické piesty

Máme dva spojené piesty naplnené nestlačiteľnou kvapalinou. To znamená, že objem kvapaliny sa nemení. Ak teda vytlačíme objem \(V\) posunutím piestu o dráhu \(h_1\), do druhého piestu musí pribudnúť taktiež objem \(V\). Ako však zistíme, o koľko sa posunul druhý piest? No to je vcelku jednoduché. Objem vody vytlačenej piestom predsa vyrátame ako: \[V=Sh\text.\]

Ak teda poznáme obsah oboch podstáv \(S_1\) a \(S_2\) a jednu dráhu \(h_1\), tak potom \[h_2 = h_1 \frac{S_1}{S_2}\text.\]

A teraz k sile. Vieme, že tlak v pieste sa rovná \[ p = \frac{F}{S}\text. \]

Samozrejme, že stále máme oba piesty naplnené rovnakou nestlačiteľnou kvapalinou, čiže tlak musí byť v oboch piestoch rovnaký. Ak teda poznáme obsah oboch podstáv \(S_1\) a \(S_2\) a jednu silu \(F_1\), tak potom \[F_2 = F_1 \frac{S_2}{S_1}\text.\]

Riešenie sústavy

Teraz, keď už vieme, ako a čo robia jednotlivé časti našej sústavy, tak môžeme odpovedať na jednotlivé otázky.

Hmotnosť závažia

Lano držíme silou \(\SI{1}{\newton}\). Prvá kladka je pevná, čiže z hľadiska sily nerobí nič.

Druhá je voľná, čiže ako sme si povedali, voľná kladka rozkladá silu na obe strany špagátu. Ak teda na jednej strane špagátu pôsobí sila \(\SI{1}{\newton}\), tak aj na druhej strane špagátu musí pôsobiť sila \(\SI{1}{\newton}\). To znamená, že výsledná sila, ktorou kladka pôsobí na piest, je \(\SI{2}{\newton}\).

Pre piest sme si povedali, že výsledná sila je \(F_2 = F_1 \frac{S_2}{S_1}\), z čoho po dosadení dostaneme

\[\begin{aligned} F_2 &= \SI{2}{\newton} \frac{4S}{S}\text,\\ F_2 &= \SI{8}{\newton}\text. \end{aligned}\]

Ďalej máme ešte jednu pevnú kladku a ďalšiu voľnú kladku. Tá pevná opäť nespraví nič. No tá voľná zasa rozloží silu, ktorou drží závažie, na obe strany. Ak teda jedna z tých strán pôsobí silou \(\SI{8}{\newton}\), tak závažie musí pôsobiť silou \(\SI{16}{\newton}\).

Ak vieme, že \[F=mg\text,\] tak potom \[m=\frac{F}{g}\text,\] a teda hmotnosť závažia je \[\begin{aligned} m &= \frac{\SI{16}{\newton}}{\SI{9.81}{\metre\per\second\squared}}\text,\\ m &= \SI{1.63}{\kilo\gram}\text. \end{aligned}\]

O koľko potiahnuť lano?

Vieme, že chceme posunúť závažie o \(\SI{1}{\centi\metre}\). Tentoraz poďme od závažia po začiatok kladkostroja. Najprv máme voľnú kladku, ktorú keď chceme zdvihnúť o \(\SI{1}{\centi\metre}\), musíme potiahnuť \(\SI{2}{\centi\metre}\). Ďalej máme pevnú kladku, ktorá žiadnym spôsobom neovplyvní, o koľko musíme potiahnuť lano. Za kladkou nasleduje piest. Ako sme si povedali, \[h_2 = h_1 \frac{S_1}{S_2}\text,\]

kde za \(h_1\) dosadíme \(\SI{2}{\centi\metre}\), \(S_1\) je plocha pri závaží, čiže \(4S\) a \(S_2\) je \(S\). Teda lano prichytené na druhý koniec piestu treba potiahnuť o \[\begin{aligned} h_2 &= \SI{2}{\centi\metre} \frac{4S}{S}\text,\\ h_2 &= \SI{8}{\centi\metre}\text. \end{aligned}\]

Ešte nám zostáva jedna voľná a jedna pevná kladka. Voľná opäť dráhu zdvojnásobí, teda aspoň v tomto smere, keďže chceme voľnú kladku zdvihnúť o \(\SI{8}{\centi\metre}\) a na to musíme potiahnuť \(\SI{16}{\centi\metre}\) lana. Pevná nespraví nič, z čoho vyplýva, že treba potiahnuť \(\SI{16}{\centi\metre}\) lana.

Koľko práce?

Otázka sa pýta: Akú prácu Marianka vykoná, ak zdvihne závažie s hmotnosťou \(\SI{1.63}{\kilo\gram}\) o \(\SI{1}{\centi\metre}\)? Túto otázku však môžeme preformulovať na: Akú prácu Marianka vykoná, ak zdvihne závažie silou \(\SI{1}{\newton}\) o \(\SI{16}{\centi\metre}\)?

Toto tvrdenie môže vyvolať otázku prečo?

No odpoveď je pomerne jednoduchá, náš kladkostroj žiadnu prácu nevykonáva, iba mení jej formu. Takže to, či zdvihneme závažie s hmotnosťou \(\SI{1.63}{\kilo\gram}\) o \(\SI{1}{\centi\metre}\), je úplne to isté, ako keby sme využili kladkostroj, a teda potiahli \(\SI{16}{\centi\metre}\) lana, silou \(\SI{1}{\newton}\), čím by sme závažie vo výsledku tiež zdvihli o \(\SI{1}{\centi\metre}\).

Keďže prácu vyrátame ako \[W = F \cdot s\text,\] tak výsledná práca je \[\begin{aligned} W &= \SI{1}{\newton} \cdot \SI{16}{\centi\metre}\text,\\ W &= \SI{1}{\newton} \cdot \SI{0,16}{\metre}\text,\\ W &= \SI{0,16}{\joule}\text. \end{aligned}\]

A teda rovnaký výsledok dostaneme, aj keď dosadíme hodnoty, ako keby sme priamo zdvíhali závažie \[\begin{aligned} W &= \SI{16}{\newton} \cdot \SI{1}{\centi\metre}\text,\\ W &= \SI{16}{\newton} \cdot \SI{0,01}{\centi\metre}\text,\\ W &= \SI{0,16}{\joule}\text. \end{aligned}\]