Zadanie
Adam si kúpil veľké rovinné nástenné zrkadlo. Keďže nechcel platiť ani o kúsok zrkadla navyše, presne si spočítal, aké veľké zrkadlo potrebuje, aby sa v ňom videl celý. Spočítal si aj to, do akej výšky má zrkadlo zavesiť. Potom sa však zdesil, keď si uvedomil, že svoje výpočty vykonal pre jednu konkrétnu vzdialenosť od zrkadla. Ale čo ak sa postaví pred zrkadlo v inej vzdialenosti? Závisia potrebné rozmery zrkadla a výška jeho zavesenia od toho, ako ďaleko sa pred zrkadlo postaví? A vlastne aké veľké zrkadlo si Adam kúpil a ako vysoko ho zavesil, ak je vysoký \(H\) a počítal so vzdialenosťou \(D\)?
Najskôr by sme sa mali zamyslieť nad tým, ako vlastne funguje rovinné zrkadlo. Zrkadlo od seba odráža svetelné lúče, a teda našimi očami môžeme pozorovať akýsi obraz telesa pred zrkadlom. Skutočnú podobu toho, čo vidíme v zrkadle, nazývame vzor. Rovinné zrkadlo narozdiel od iných má ešte tú špeciálnu vlastnosť, že obraz je rovnako veľký ako vzor - teda obraz je zhodný so vzorom.
Zobrazovanie v rovinnom zrkadle si vieme jednoducho predstaviť ako osové preklopenie cez zrkadlo. Keď sa teda Adam postavil pred zrkadlo, mohlo by to vyzerať asi takto:
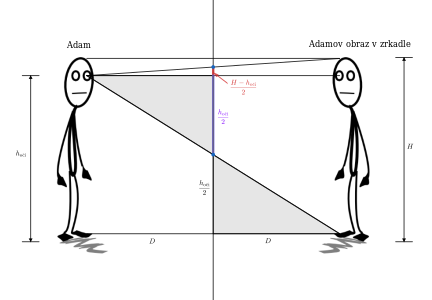
Označme si výšku, v ktorej má Adam oči, ako \(h_{\mathrm{oči}}\). Z tejto výšky sa Adam pozerá do zrkadla, kde by sa chcel vidieť celý. To znamená, že chce vidieť svoje chodidlá a zároveň svoje vlasy. Ako máme dať zrkadlo, aby sa mu splnilo jeho želanie? Najskôr sa pozrime, v akej výške musí byť spodok zrkadla, aby Adam videl na svoje chodidlá.
Na to, aby Adam uvidel svoje chodidlá, musí zrak sklopiť tak, že sa bude pozerať na úroveň podlahy vo vzdialenosti \(D\) „za zrkadlom“. Geometricky to pre nás znamená, že spojíme úsečkou oko vzoru a chodidlo obrazu, čím znázorníme Adamov pohľad. Táto úsečka sa nám v nejakom bode pretne so zrkadlom (v obrázku je to spodný modrý bod). Znamená to, že v tejto výške sa už musí nachádzať zrkadlo. Keď sa však na obrázok lepšie pozrieme, uvedomíme si, že sivé trojuholníky sú zhodné, a preto vzdialenosť od podlahy k spodku zrkadla je rovnaká ako fialová vzdialenosť. No a keďže ich súčet je \(h_{\mathrm{oči}}\), dĺžka fialovej úsečky bude \(\frac{h_{\mathrm{oči}}}2\).
Keď sa teraz chce pozrieť na svoje vlasy, musí sa pozrieť do výšky \(H\) a vzdialenosti \(D\) za zrkadlom. Keď spojíme oko vzoru s najvyšším bodom obrazu, pretnú nám zrkadlo v hornom modrom bode. Toto musí byť najvyšším bodom hľadaného zrkadla, pretože inak by Adam vrch svojej hlavy v zrkadle nevidel. Keď si znovu všimneme dva zhodné trojuholníky, nebude pre nás problémom vypočítať, že dĺžka červenej úsečky je rovná polovici výškového rozdielu medzi očami a úpätím hlavy - a teda \(\frac{H-h_{\mathrm{oči}}}2\).
Našli sme teda najmenšie zrkadlo, v ktorom sa Adam uvidí celý. Jeho výšku vieme vypočítať ako súčet dĺžok červenej a fialovej úsečky, čo vychádza ako
\[h_{\mathrm{zrkadlo}}=\frac{H-h_{\mathrm{oči}}}2+\frac{h_{\mathrm{oči}}}2=\frac H2\text.\]
Toto zrkadlo treba zavesiť do výšky, ktorá je o \(\frac{H-h_{\mathrm{oči}}}2\) menšia ako Adamova výška.
Ešte však treba zodpovedať na jednu otázku: Závisia potrebné rozmery zrkadla od vzdialenosti \(D\)? Keď sa pozrieme na to, aké výsledky nám vyšli, ani v jednom z nich nevystupuje \(D\). To znamená, že potrebné rozmery zrkadla nezávisia od vzdialenosti \(D\).
Diskusia
Tu môžte voľne diskutovať o riešení, deliť sa o svoje kusy kódu a podobne.
Pre pridávanie komentárov sa musíš prihlásiť.