4. Stop plytvaniu! vzorové riešenie

V zadaní máme, že odpor je priamo úmerný dĺžke¹. Preto si vieme zapísať, že \[ R = cl \] pre nejakú konštantu úmernosti \(c\) medzi odporom a dĺžkou vodiča. Na začiatok by bolo zaujímavé zistiť, aký prúd prechádza pôvodnou šípkou. Na to si na ňu budeme musieť posvietiť.

Ako si zjednodušiť úlohu?

Keď máme úlohu s elektrickými obvodmi, tak sa častokrát snažíme porozkladať si obvod na jednoduchšie časti, ktoré sú buď v sériovom alebo paralelnom zapojení, pretože na tie poznáme vzorčeky, a teda sa už potom dopočítame k výsledku. Kurzor na prvý pohľad vyzerá na paralelné zapojenie, no kazí nám to tam jeden vodič (na obrázku 1 znázornený červenou), ktorý vetvy prepája.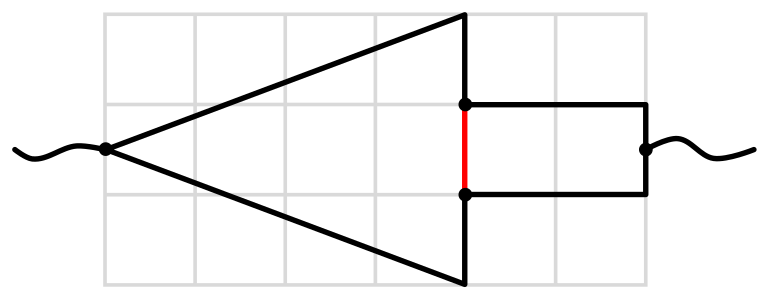

Keď sa však na schému lepšie zahľadíme, tak si všimneme, že je horizontálne symetrická. Čo to ale ovplyvní? Do obidvoch uzlov, v ktorých má červený vodič počiatok, kvôli symetrii tečie rovnaké množstvo prúdu. Tieto dva uzly potom majú rovnaké potenciály, a teda napätie medzi nimi (čiže rozdiel potenciálov okrajových uzlov) je nulový. No a z toho, že napätie je nulové, už podľa Ohmovho zákona ľahko prídeme na to, že prúd pretekajúci týmto vodičom je \(I=\frac UR=\frac0R=0\). Trochu iný pohľad do tejto problematiky je, že nakoľko do okrajových uzlov vteká rovnaký prúd, tak aj do červeného vodiča z oboch uzlov vteká rovnaký prúd. Tieto prúdy sa nám ale navzájom vynulujú, a teda výsledný prúd pretekajúci vodičom je nulový. Ako sme si týmto pomohli? Nakoľko nás zaujíma, aký prúd preteká obvodom, tak nakoľko červeným vodičom prúd nepreteká, môžeme ho z obvodu odstrániť. Následne už dostaneme paralelné zapojenie, ktoré vieme jednoducho dopočítať.

Aký prúd prechádza pôvodným kurzorom?

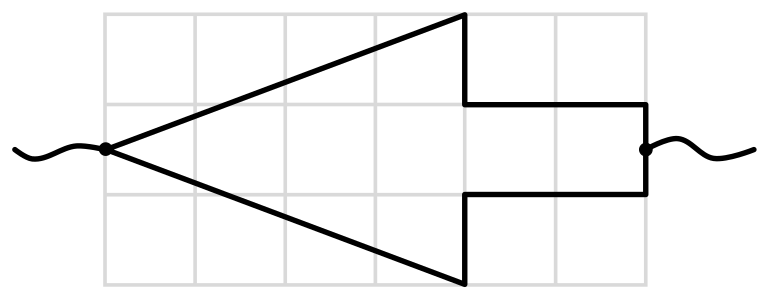
Nakoľko už máme obvod v stave, že ide o paralelné zapojenie, môžeme sa pustiť do počítania odporu kurzora. Nakoľko odpor je závislý od dĺžky drôtu, musíme zistiť, aký dlhý je drôt vo vetvách. Využijeme pri tom, že prepona pravouhlého trojuholníka sa z Pytagorovej vety dá vypočítať ako \(c=\sqrt{a^2+b^2}\). Dĺžka drôtu jednej vetvy je: \[ l_{\mathrm{vetva}}=\frac12 a + 2a + a + \sqrt{\left(\frac32a\right)^2+(4a)^2}=\frac72a + \sqrt{\frac94a^2+\frac{64}4a^2}=\frac72a+\frac{\sqrt{73}}2a=\frac{7+\sqrt{73}}2\cdot a\text. \] Potom odpor jednej vetvy vypočítame ako: \[ R_{\mathrm{vetva}}=cl_{\mathrm{vetva}}=\frac{7+\sqrt{73}}2\cdot ac\text. \] No a nakoniec pre celkový odpor \(R\) obvodu platí: \[ \begin{aligned} \frac1R&=\frac1{R_{\mathrm{vetva}}}+\frac1{R_{\mathrm{vetva}}}\text,\\ &=\frac2{R_{\mathrm{vetva}}}\text,\\ R&=\frac12R_{\mathrm{vetva}}=\frac{7+\sqrt{73}}4\cdot ac\text. \end{aligned} \]

Aký tvar drôtu spotrebuje najmenej materiálu?

Keďže kurzor je vlastne paralelné zapojenie, tak intuitívne to vyzerá tak, že najmenšie plytvanie materiálom dosiahneme pri sériovom zapojení, t.j. keď drôt nebude obsahovať žiadne uzly. Bolo by však vhodné toto tvrdenie aj nejako zdôvodniť. Zoberme si teda nejaké zapojenie, ktoré je rozvetvené a prúdi ním rovnaký prúd, ako prúdil kurzorom. Teraz si zoberme dve časti obvodu s odpormi \(R_1,R_2\), ktoré sú zapojené paralelne. Ich odpor vieme vypočítať ako \[ R_p=\frac1{\frac1{R_1}+\frac1{R_2}}\text. \] Keby sme však tieto dve časti obvodu preskupili a dali ich do sériového zapojenia, tak by sme tým dosiahli odpor \[ R_s=R_1+R_2\text. \] Teraz ukážeme, že \(R_s>R_p\) pre akékoľvek hodnoty \(R_1,R_2\). \[ R_s=R_1+R_2>R_1=R_1\cdot1>R_1\frac{R_2}{R_1+R_2}=\frac{R_1R_2}{R_1+R_2}=\frac1{\frac{R_1+R_2}{R_1R_2}}=\frac1{\frac1{R_1}+\frac1{R_2}}=R_p\text. \] Toto je samozrejme len jeden z množstva spôsobov, akým sa dala táto nerovnosť dokázať.² Ak by sme takýto postup opakovali, dokým by bolo čo preskupovať, dosiahli by sme stav sériového zapojenia, ktorý by mal ostro väčší odpor ako obvod na začiatku. Nakoľko však napätie zdroja je konštantné a okrem toho potrebujeme, aby obvodom pretekal rovnaký prúd ako predtým, tak z Ohmovho zákona máme, že aj odpor obvodu musí byť rovnaký. Preskupovaním paralelných zapojení do sériových sa nám však odpor zvyšoval, a aby sme ho znížili, potrebujeme skrátiť dĺžku získaného drôtu. Z vyššie uvedených informácii vidíme, že pri sériovom zapojení spotrebujeme najmenej materiálu.

Záver

Ešte by nás zaujímalo, koľkokrát menej drôtu sme použili. Ako sme už vyššie ukázali, odpor musí byť rovnaký ako v pôvodnom kurzore, aby sa zachovala aj hodnota prúdu. Preto platí \(R_{\mathrm{vylepšenie}}=R=\frac{7+\sqrt{73}}4\cdot ac\). Nakoľko ale v našom vylepšení využívame iba jeden drôt bez uzlov, tak jeho odpor je priamo úmerný dĺžke (a rovnako aj dĺžka je priamo úmerná odporu)³, a teda si dľžku drôtu po vylepšení vieme vypočítať ako \[ l_{\mathrm{vylepšenie}}=\frac{R_{\mathrm{vylepšenie}}}c=\frac{7+\sqrt{73}}4\cdot a\text. \] Nuž a keď si spomenieme, že dĺžku vetvy kurzora sme už počítali (netreba však zabudnúť na vodič, ktorý sme si vymazali), tak dĺžku drôtu spotrebovaného na kurzor vypočítame ako \[ l_{\mathrm{kurzor}}=2l_{\mathrm{vetva}}+a=(8+\sqrt{73})a\text. \] Pomer dĺžok drôtov použitých na odporové siete je teda \[ \eta=\frac{l_{\mathrm{kurzor}}}{l_{\mathrm{vylepšenie}}}\approx\num{4.25}\text. \] Dosiahli sme viac ako štvornásobné zlepšenie, sme teda so sebou spokojní a môžeme sa pustiť do ďalšej úlohy.

---

1. túto informáciu vieme zapísať aj ako \(R\propto l\) - značenie \(\propto\) hovorí o priamej úmere medzi dvoma veličinami↩

2. Ak vás baví matematika, tak vás možno zaujme, že táto nerovnosť sa dala dokázať aj pomocou nerovnosti medzi aritmetickým a harmonickým priemerom (často označovanej aj ako AH nerovnosť). Môžete sa o to pokúsiť aj vy. Viac o nej si môžete prečítať na https://cs.wikipedia.org/wiki/Nerovnosti_mezi_pr%C5%AFm%C4%9Bry.↩

3. Pre funkcie \(f,g\) platí \(f\propto g\iff g\propto f\), pretože ak je \(f\) priamoúmerná \(g\) s konštantou úmernosti \(c\), tak \(g\) je priamoúmerná \(f\) s konštantou úmernosti \(\frac1c\).↩