5. O Lukášoch a hojdačkách vzorové riešenie

Zadanie

Počas dlhých letných dní si treba úžívať pobyt vonku. Lukáš s Lukášom¹ to tiež dobre vedia a radi sa chodia zabávať na ihrisko. Všimli si, že na ihrisku pribudli dve nové hojdačky. Nevedeli sa však rozhodnúť, na ktorú z nich sa pôjdu pohojdať. V rozhodovaní by im pomohlo, keby vedeli, aký je rozdiel v spôsobe hojdania sa na nich. Pomôžte Lukášom v rozhodovaní a vysvetlite im, aký je rozdiel v hojdaní sa na týchto dvoch rôznych hojdačkách.

Skúste sa poriadne zamyslieť nad momentami síl a stabilitou hojdačiek.

---

1. Gáborik a Obermajer↩

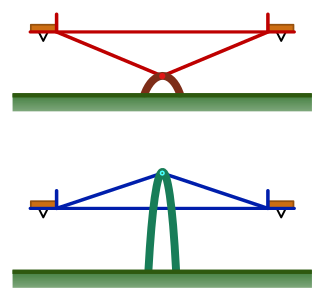
Ako prvé sa pozrieme, v akých rovnovážnych polohách sú hojdačky. V prvom prípade je bod otáčania tesne nad zemou a ťažisko nad ním. V druhom prípade je bod otáčania zjavne vyššie ako ťažisko hojdačky. Teraz si predstavme, že do hojdačiek niečo udrie alebo zafúka vietor. Ťažisko oboch hojdačiek sa kúsok vychýli. V prvom prípade však gravitačná sila začne hojdačku pretáčať, až kým jedna strana nepadne na zem. V druhom prípade začne gravitačná sila pretáčať hojdačku naspäť do pôvodnej polohy. Prvá hojdačka je labilná a druhá stabilná¹.

Ďalej sa zamyslíme, čo sa stane, ak si na hojdačku sadnú obaja chlapci za predpokladu, že sú podobne ťažkí. Prvá hojdačka sa pravdepodobne pri nasadaní prevráti na jednu stranu. Aby sa chlapci mohli hojdať, musí sa vždy jeden odraziť nohami dosť silno, aby dostal ťažisko nad bod otáčania a až na druhú stranu. Ak by bol jeden výrazne ťažší, hojdačka by sa stále prevrátila na jeho stranu, pretože by ťažisko bolo bližšie pri ňom a nemohlo by sa dostať nad bod otáčania.

Druhá hojdačka sa bude správať podobne ako kyvadlo. Ak sa jeden z chlapcov odrazí, posunie hojdačku z rovnovážnej polohy. Ťažisko posunie spopod bodu otáčania a hojdačka sa bude snažiť dostať späť do polohy, kde bola, ale začne sa hojdať podobne ako kyvadlo. Samozrejme raz za čas sa bude musieť jeden z chlapcov odraziť, pretože hojdačka bude spomaľovať z dôsledku odporu vzduchu a  trenia v bode otáčania.

Poznámka ku momentom síl: Keďže obe hojdačky majú rovnako dlhé ramená, takže aj momenty síl budú rovnaké na oboch hojdačkách v začiatočnej pozícii. Počas hojdania sa budú momenty síl meniť pretože sila nebude pôsobiť kolmo na rameno. Tieto zmeny momentov budú hojdačku dva stabilizovať a hojdačku jedna destabilizovať. Nakoľko tento jav je nad rámec základnej školy, nebudeme ho uvažovať pri hodnotení.