Zadanie
Letné počasie prichádza aj s letnými búrkami. Marcel si pri testovaní, v akej vzdialenosti blesk udrel1, uvedomil, že nepočujeme hrom len na jednom mieste. Preto sa rozhodol, že si spraví model blesku, ktorý od začiatku až po koniec hrmí v každom bode svojho putovania cez vzduch. Potom si počkal na blesk, ktorý išiel kolmo z oblaku do zeme, a začal počítať. Napočítal \(8\) sekúnd od záblesku po hrom, a potom ešte dalšie \(4\) sekundy hrmenia. Ako vysoko nad zemou blesk začal svoju púť?
Čas, za ktorý blesk po opustení oblaku dosiahne zemský povrch, je zanedbateľný voči času, za ktorý zvuk hromu dorazí k Marcelovi.
Vzdialenosť vieme určiť ako počet sekúnd od záblesku až po počutie hromu vynásobený rýchlosťou zvuku, \(\SI{330}{\metre\per\second}\).↩︎
Podľa zadania uvažujeme, že blesk prejde každým miestom dráhy v prakticky rovnakom okamihu a v každom mieste vytvorí len na malú chvíľku (nie na dlhší časový interval) zvuk hrmenia.
Zvuk je nejaké vlnenie vzduchu, ktoré zdroj zvyčajne vyšle do všetkých smerov. K nám dorazí tá časť tohto vlnenia, ktorá na nás priamo smeruje, t.,j. šíri sa po priamej spojnici medzi zdrojom a nami. Po tejto spojnici vlnenie cestuje práve rýchlosťou zvuku, ktorá závisí na látke, ktorá sa vlní. Pre vzduch je táto rýchlosť šírenia vlnenia približne \(\SI{330}{\metre\per\second}\).
Keďže hrmenie na každom mieste dráhy blesku trvá len chvíľku, dôvod, prečo počujeme hrom trvajúci niekoľko sekúnd je, že z rôznych miest k nám dorazí zvuk v rôznych časoch a vytvára tak dojem spojitého hrmenia.
Pri blesku, ktorý udrie z oblaku kolmo na miesto na zemi pod ním, práve hrmenie z toho miesta, kde sa blesk stretáva so zemou, budeme počuť ako prvé (lebo má od nás iba horizontálnu vzdialenosť, nemá vertikálnu vzdialenosť).
Ďalej budeme hrmenie počuť z ďalších miest po dráhe blesku, stále vyšších a vyšších.
Úplne nakoniec k nám dorazí zvuk z miesta, kde blesk v oblaku začína, nakoľko to je od nás najvzdialenejšie – okrem vzdialenosti rovnobežnej na povrch Zeme (horizontálnej vzdialenosti), ktorá je pre všetky miesta po dráhe nášho kolmého blesku rovnaká, má spomedzi všetkých miest na dráhe blesku najväčšiu vertikálnu vzdialenosť – je v najväčšej výške vzhľadom na našu pozíciu.
Predstavme si to na nákrese:
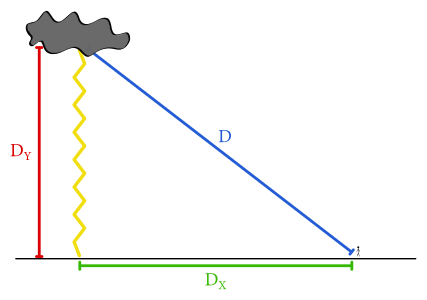
Horizontálnu vzdialenosť (\(D_{\mathrm{x}}\)) blesku od nás určíme ako \(\SI{8}{\second} \cdot \SI{330}{\metre\per\second} = \SI{2640}{\metre}\), pretože zvuku trvalo túto vzdialenosť prejsť rýchlosťou \(\SI{330}{\metre\per\second}\) osem sekúnd.
Vzdialenosť od najvyššieho bodu blesku až k nám trvalo zvuku prejsť zase až dvanásť sekúnd. Celková vzdialenosť (\(D\)) bola teda \(\SI{330}{\metre\per\second} \cdot \SI{12}{\second} = \SI{3960}{\metre}\). Ale ako z tohto vypočítame výšku, t.,j. vertikálnu vzdialenosť (\(D_{\mathrm{y}}\))?
Nakoľko blesk udrel na zem kolmo, horizontálna vzdialenosť a vertikálna vzdialenosť tvoria odvesny pravouhlého trojuholníka, zatiaľ čo celková vzdialenosť je preponou.
Zostrojíme rovnicu podľa Pytagorovej vety: \[D^2 = D_{\mathrm{x}}^2 + D_{\mathrm{y}}^2,\] z čoho vyjadríme \[D_{\mathrm{y}}^2 = D^2 - D_{\mathrm{x}}^2\] a nakoniec \[D_{\mathrm{y}} = \sqrt{D^2 - D_{\mathrm{x}}^2}.\]
Dosadíme \(D = \SI{3960}{\metre}\) a \(D_{\mathrm{x}} = \SI{2640}{\metre}\).
Zistíme, že \(D_{\mathrm{y}} = \SI{2951}{\metre}\), blesk teda začal približne v troch kilometroch nad zemou.
Diskusia
Tu môžte voľne diskutovať o riešení, deliť sa o svoje kusy kódu a podobne.
Pre pridávanie komentárov sa musíš prihlásiť.