2. No moment, prekážka! vzorové riešenie

Zadanie

Lukáš pri behu po prekážkovej dráhe narazil na nasledujúcu prekážku. Nachádzala sa pred ním veľká jama, široká \(10\) metrov, ktorú potreboval prejsť. Porozhliadol sa po okolí, či by mu niečo nevedelo pomôcť a uvidel rozložený rebrík v tvare V s vnútorným uholom \(\SI{120}{\degree}\) a ramenami dlhými \(30\) metrov a \(10\) metrov. Keďže Lukáš nie je len šikovný bežec, ale aj fyzik, tak mu veľmi rýchlo napadlo riešenie jeho problému a zabehol si po rebrík. Postavil si ho pred jamu tak, že dlhšie rameno ležalo na zemi a ohyb sa nachádzal na okraji jamy (viď obrázok) a začal sa šplhať. Po chvíli šplhania sa rebrík prevážil cez jamu a Lukáš mohol spokojne pokračovať v behu. Ako vysoko sa musel Lukáš vyšplhať po rebríku, aby ho prevážil, ak dĺžková hmotnosť rebríka je \(\SI{0,7}{\kilo\gram\per\meter}\) a Lukáš váži \(\SI{85}{\kilo\gram}\)?

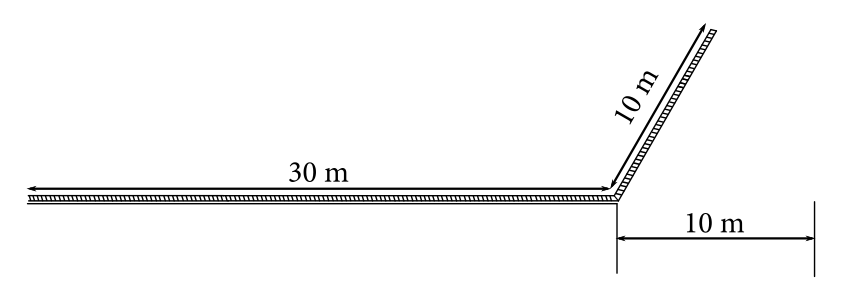
Ako našu sústavu si zvolíme rebrík a Lukáša. Prečo práve túto sústavu? Lebo sa budeme pozerať len na vonkajšie sily pôsobiace na sústavu, takže nebudeme musieť riešiť silové pôsobenie medzi Lukášom a rebríkom.

Úlohu vieme riešiť viacerými spôsobmi. Tu si ukážeme riešenie pomocou ťažiska a riešenie pomocou momentov síl.

Riešenie pomocou ťažiska

Naša sústava bude stabilná, keď sa jej ťažisko bude nachádzať medzi koncami dotykových plôch rebríka so zemou. Keď sa už bude nachádzať nad jamou, tak rebrík začne padať do jamy, aby sa mu znížila potenciálna energia. Ak si za počiatok súradnicovej sústavy zvolíme ohyb rebríku a kladný smer osi \(x\) ako smer doprava (k jame), tak sa rebrík prevráti, keď bude platiť

\[ x_T >0 \]

kde \(x_T\) je \(x\)-ová súradnica polohy ťažiska. Budú nás zaujímať len \(x\)-ové súradnice, lebo len od nich závisí, kedy sa rebrík prevráti. Označme si \(m_1\) hmotnosť dlhšieho ramena rebríka a \(l_1\) jeho polovičnú dĺžku. Obdobne si označíme aj pre kratšie rameno ako \(m_2\) a \(l_2\). Pre Lukáša si zavedieme jeho hmotnosť \(m\) a vzdialenosť od ohybu po Lukáša \(l\). Posledné označenie bude susedný uhol k vnútornému uhlu rebríka ako \(\alpha\).

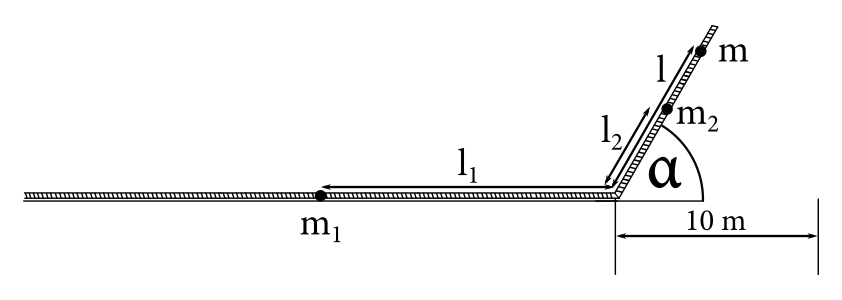
Pre výpočet \(x_T\) si budeme musieť vypočítať \(x_1\), \(x_2\) a \(x\). Pre \(x_1\) dostaneme \(x_1=-l_1\). Pre \(x_2\) už budeme musieť použiť trigonometriu a dostaneme \(x_2=l_2 \cos \alpha\). Pre \(x\) znovu použijeme trigonometriu a dostaneme \(x=l \cos \alpha\).

Polohu ťažiska si potom vypočítame ako vážený priemer hmotností častíc v sústave podľa ich vzdialenosti. Dostaneme teda

\[ \begin{aligned} x_T &=\frac{m_1 x_1+m_2 x_2 +m x}{m_1+m_2+m}\\ x_T &=\frac{-m_1 l_1+m_2 l_2 \cos \alpha+m l \cos \alpha} {m_1+m_2+m} \end{aligned} \]

Vieme, že aby sa rebrík prevrátil, musí platiť \(x_T>0\). Preto dostaneme nerovnicu

\[ \frac{-m_1 l_1+m_2 l_2 \cos \alpha+m l \cos \alpha} {m_1+m_2+m} > 0 \]

Túto nerovnicu si postupnými úpravami vyriešime. Nezabúdajte, že všetky hmotnosti aj vzdialenosti sú kladné čísla, takže nemusíme riešiť otáčanie nerovnice.

\[ \begin{aligned} -m_1 l_1+m_2 l_2 \cos \alpha+m l \cos \alpha &> 0 \\ m l \cos \alpha &> m_1 l_1-m_2 l_2 \cos \alpha \\ l &> \frac{m_1 l_1-m_2 l_2 \cos \alpha}{m \cos \alpha} \end{aligned} \]

Hmotnosti \(m_1\) a \(m_2\) si vieme vyjadriť pomocou ich dĺžok \(2l_1\), \(2l_2\) a dĺžkovej hmotnosti \(\mu\) ako \(m_1=2l_1 \mu\) a \(m_2=2l_2\mu\). Po dosadení vyjadrení dostaneme

\[ \begin{aligned} l &> \frac{2\mu}{m} \left( \frac{1}{\cos \alpha} l_1^2 -l_2^2 \right) \\ l &> \SI{7}{\metre} \end{aligned} \]

Preto Lukáš musí vyliezť po rebríku viac ako \(7\) metrov. Musel sa preto vyšplhať do výšky viac ako \(l \sin \alpha\), teda viac ako \(6.06\) metrov.

Riešenie pomocou momentov síl

Na začiatok uvediem, že budeme pracovať s veľkosťami síl, ale nazývať ich budeme len silami. Vonkajšie sily, ktoré nám pôsobia na sústavu sú gravitačná sila prvého ramena \(F_{g_1}=m_1g\), gravitačná sila druhého ramena \(F_{g_2}=m_2g\), gravitačná sila pôsobiaca na Lukáša \(F_g=mg\) a normálová sila od zeme \(F_N= F_{g_1}+F_{g_2}+F_{g}\). Gravitačné sily majú pôsobisko v daných ťažiskách a normálová sila na mieste dotyku rebríka so zemou. Toto miesto bude pod ohybom rebríka, lebo to bude jediné miesto dotyku rebríka zo zemou v momente, keď sa rebrík preváži.

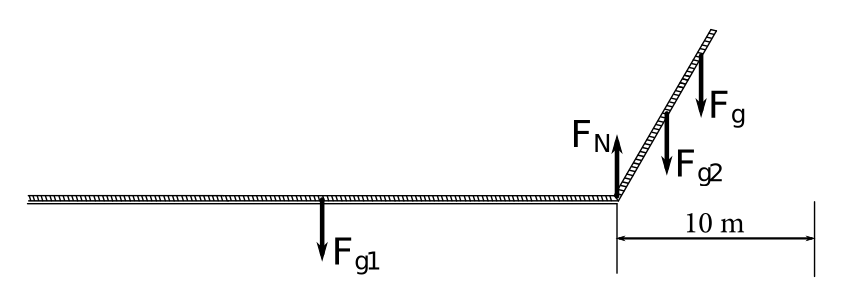
Našu sústavu si vieme predstaviť ako páku, ktorá má os otáčania v bode ohybu rebríka. A uhol, ktorý zvierajú ramená, nie je \(\ang{180}\), ale len \(\ang{120}\). Preto na určenie kolmých vzdialeností budeme musieť v niektorých prípadoch použiť trigonometriu.

Rebrík sa preváži smerom do jamy. Tento smer je v smere hodinových ručičiek, čiže záporný smer. Preto pre výsledný moment síl bude platiť.

\[ M < 0 \]

Pre výpočet \(M\) si budeme musieť vypočítať \(M_1\), \(M_2\), \(M_L\) a \(M_N\). Pre \(M_1\) dostaneme \(M_1=F_{g_1}l_1\). Pre \(M_2\) už budeme musieť použiť trigonometriu a dostaneme \(M_2=-F_{g_2}l_1 \cos \alpha\). Pre \(M_L\) znovu použijeme trigonometriu a dostaneme \(M_L=-F_{g}l \cos \alpha\). Pre \(M_N\) dostaneme \(\SI{0}{\newton\metre}\), lebo normálová sila má pôsobisko v osi otáčania.

Dostaneme teda

\[ \begin{aligned} M_1+M_2+M_L &< 0 \\ F_{g_1}l_1-F_{g_2}l_1 \cos \alpha-F_{g}l \cos \alpha &< 0 \\ m_1gl_1-m_2gl_1 \cos \alpha-mgl \cos \alpha &< 0 \\ -m_1 l_1+m_2 l_2 \cos \alpha+m l \cos \alpha &> 0 \end{aligned} \]

Dostali sme nerovnicu, ktorú sme už mali vyššie, preto vieme, že sa úpravami dostaneme k rovnakému výsledku.