Zadanie
Marek sa po poslednej prechádzke v lese začal hrať s papekmi. Pripevnil koniec krátkeho konára v lese na klinec, tak, že sa mohol okolo neho otáčať. Konár sa následne udomácnil v rovnovážnej polohe (čiže len tak zvislo visel).
Následne Marek do konára jemne drgol (konár sa nevychýlil veľmi) a tým sa konár začal pravidelne pohybovať okolo rovnovážnej polohy. Marek odmeral čas, ktorý konáru trvá, kým sa dostane z rovnovážnej polohy opäť do rovnovážnej polohy. Následne začal z konára postupne odlamovať, čím sa začal meniť aj čas, ktorý konáru trvá, kým prekmitne okolo rovnovážnej polohy.
Vyhliadnite si vo svojom okolí konár alebo niečo jemu tvarom podobné a odmerajte, ako závisí čas prekmitnutia okolo rovnovážnej (zvislej) polohy od dĺžky konára.
Každého fyzika musí po prečítaní zadania trknúť, že Marek si postavil kyvadlo. Nejedná sa však o obyčajné kyvadlo, s akým sa môžete stretnúť napríklad na hodinách fyziky. Konár Marekovho kyvadla slúži ako záves a zároveň ako závažie, ktoré na závese kmitá.
Naopak, pre klasické (matematické) kyvadlo platí, že závažie je malé (ideálne bodové) a hmotnosť závesu je oproti závažiu zanedbateľná (ideálne nulová). Pre periódu1 \(T_\mathrm{m}\) matematického kyvadla platí jednoduchý vzťah, ktorá závisí len na dĺžke závesu \(l\) a tiažovom zrýchlení \(g\): \[T_\mathrm{m} = 2\pi \sqrt{l/g}\text{.}\] Môžeme si všimnúť, že perióda nezávisí na hmotnosti závažia a je úmerná odmocnine z dĺžky závesu.
Z dôvodu, že Marekovo kyvadlo má hmotnosť rozloženú iným spôsobom, ako matematické kyvadlo, môžeme usúdiť, že jeho doba kyvu bude iná, ako čas \(T_\mathrm{m}/2\). Ak začneme konár skracovať, budeme tým meniť nielen len dĺžku „závesu“, ale zároveň aj hmotnosť „závažia“. Predpovedať, ako sa pri tejto operácii bude meniť doba kyvu, je preto komplikovaná záležitosť. Dúfajme preto, že samotné meranie nám prinesie viac informácií.
Zmerať dobu kmitu (hocijakého) kyvadla nie je vôobec náročné. Ako sa píše v zadaní, kyvadlo najskôr zostrojíme. V našom prípade bola dobrým prototypom konáru drevená špajdľa, ktorá je rovná, má homogénne rozloženú hmotu a ľahko sa meria a skracuje. Následne kyvadlo trochu vychýlime (o uhol približne 10°) a sledujeme, ako kyvadlo kmitá. Odmerať dĺžku jedného kmitu je teoreticky možné, no veľmi nepraktické. Okom totiž len ťažko odhadneme, kedy presne kyvadlo dosiahlo maximálnu výchylku. Naviac meranie je ovplyvnené pomerne veľkou reakčnou dobou človeka (\(\SI{0.2}{\second}\) až \(\SI{0.4}{\second}\)), čo je nepresnosť porovnateľná so samotnou dobou jedného kmitu.
Vylepšenie, ktoré výrazne zmenší obe spomínané chyby, je meranie doby niekoľkých kmitov. V našom prípade sme merali dobu vždy 20 kmitov, takže dobu jedného kyvu \(T/2\) sme získali vydelením nameraného času štyridsiatimi. Meranie sme opakovali pre špajdľu, ktorej pôvodnú dĺžku \(\SI{29.7}{\centi\meter}\) (vzdialenosť od osi otáčania) sme skracovali o \(\SI{1}{\centi\meter}\) až na dĺžku \(\SI{9.7}{\centi\meter}\).
Namerané hodnoty časov \(20T\) (doba 20 kmitov), ako aj doby jedného kyvu \(T/2\) v závislosti na dĺžke \(l\) špajdle uvádzame v tabuľke. Naviac sme do predposledného stĺpca tabuľky vypočítali odpovedajúcu dobu kyvu matematického kyvadla \(T_\mathrm{m}/2\) a v poslednom stĺpci tabuľky sme vypočítali pomer týchto dôb \(T/T_\mathrm{m}\). Naviac sme dobu kyvu \(T/2\) vyniesli do grafu v závislosti na dĺžke špajdle \(l\).
| \(l\ [\si{\centi\metre}]\) | \(20 T\ [\si{\second}]\) | \(T/2\ [\si{\second}]\) | \(T_\mathrm{m}/2\ [\mathrm{s}]\) | T / T_m$ |
|---|---|---|---|---|
| \(\num{29.7}\) | \(\num{17.3}\) | \(\num{0.432}\) | \(\num{0.547}\) | \(\num{0.79}\) |
| \(\num{28.7}\) | \(\num{17.0}\) | \(\num{0.424}\) | \(\num{0.537}\) | \(\num{0.79}\) |
| \(\num{27.7}\) | \(\num{17.1}\) | \(\num{0.428}\) | \(\num{0.528}\) | \(\num{0.81}\) |
| \(\num{26.7}\) | \(\num{16.8}\) | \(\num{0.420}\) | \(\num{0.518}\) | \(\num{0.81}\) |
| \(\num{25.7}\) | \(\num{16.6}\) | \(\num{0.416}\) | \(\num{0.508}\) | \(\num{0.82}\) |
| \(\num{24.7}\) | \(\num{16.2}\) | \(\num{0.405}\) | \(\num{0.498}\) | \(\num{0.81}\) |
| \(\num{23.7}\) | \(\num{16.0}\) | \(\num{0.399}\) | \(\num{0.488}\) | \(\num{0.82}\) |
| \(\num{22.7}\) | \(\num{15.6}\) | \(\num{0.389}\) | \(\num{0.478}\) | \(\num{0.81}\) |
| \(\num{21.7}\) | \(\num{15.1}\) | \(\num{0.377}\) | \(\num{0.467}\) | \(\num{0.81}\) |
| \(\num{20.7}\) | \(\num{14.8}\) | \(\num{0.369}\) | \(\num{0.456}\) | \(\num{0.81}\) |
| \(\num{19.7}\) | \(\num{14.4}\) | \(\num{0.360}\) | \(\num{0.445}\) | \(\num{0.81}\) |
| \(\num{18.7}\) | \(\num{14.0}\) | \(\num{0.350}\) | \(\num{0.434}\) | \(\num{0.81}\) |
| \(\num{17.7}\) | \(\num{13.7}\) | \(\num{0.341}\) | \(\num{0.422}\) | \(\num{0.81}\) |
| \(\num{16.7}\) | \(\num{13.5}\) | \(\num{0.336}\) | \(\num{0.410}\) | \(\num{0.82}\) |
| \(\num{15.7}\) | \(\num{12.9}\) | \(\num{0.324}\) | \(\num{0.397}\) | \(\num{0.81}\) |
| \(\num{14.7}\) | \(\num{12.5}\) | \(\num{0.313}\) | \(\num{0.385}\) | \(\num{0.81}\) |
| \(\num{13.7}\) | \(\num{12.2}\) | \(\num{0.304}\) | \(\num{0.371}\) | \(\num{0.82}\) |
| \(\num{12.7}\) | \(\num{11.6}\) | \(\num{0.291}\) | \(\num{0.357}\) | \(\num{0.81}\) |
| \(\num{11.7}\) | \(\num{11.1}\) | \(\num{0.278}\) | \(\num{0.343}\) | \(\num{0.81}\) |
| \(\num{10.7}\) | \(\num{10.5}\) | \(\num{0.264}\) | \(\num{0.328}\) | \(\num{0.80}\) |
| \(\num{9.7}\) | \(\num{10.3}\) | \(\num{0.256}\) | \(\num{0.312}\) | \(\num{0.82}\) |
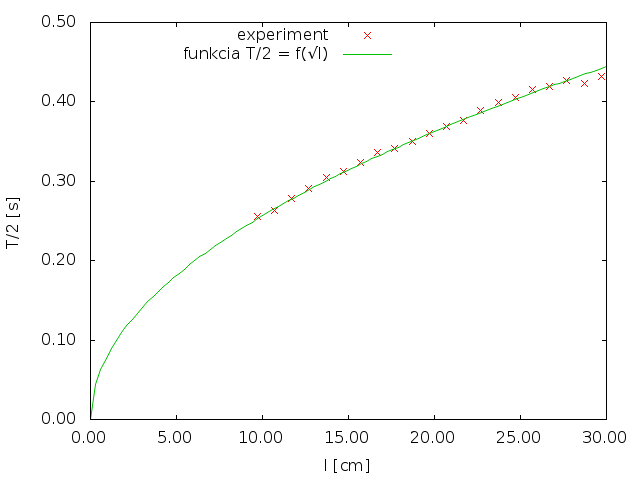
Z tabuľky si môžeme všimnúť jednu zaujímavú vec: pomer \(T/T_\mathrm{m}\) sa s meniacou dĺžkou (v rámci nepresnosti merania) nemení. To ale znamená, že pre vzťah pre dobu \(T\) platí \(T = k T_\mathrm{m}\), kde \(k\) práve zmeraný pomer. Inými slovami, už teraz vieme povedať, že doba jedného kyvu Marekovho konára závisí, rovnako ako v prípade matematického kyvadla, na odmocnine z dĺžky konára. Túto závislosť môžeme s trochou predstavivosti vidieť aj v grafe. Pre väčšiu predstavivosť sme namerané dáta naozaj preložili (správne naškálovanou) funkciou \(T/2 = f(\sqrt{l})\).
Vo vyšších ročníkoch, na sústredku FKS alebo na sústredení fyzikálnej olympiády sa určite naučíte, že perióda Marekovho kyvadla sa dá zistiť aj teoreticky, práve pre prípad kmitajúcej homogénnej paličky. Presne ako v experimente zistíme, že pomer \(T/T_\mathrm{m}\) je konštantný a rovný \(\sqrt{2/3} \doteq \num{0.82}\). Zhoda s experimentom je teda perfektná. Na záver len dodajme, že iné výsledky by sme dostali, ak by sme experiment uskutočnili s reálnym konárom, ktoré má, narozdiel od špajle, hmotu rozloženú vzhľadom k osi otáčania ešte komplikovanejšie.
Perióda je čas medzi dvomi po sebe nasledujúcimi návratmi kyvadla do tej istej krajnej polohy (teda doba jedného kmitu). V zadaní nás zaujíma ale doba medzi dvomi prekmitnutiami cez rovnovážnu, tzn. zvislú polohu, ktorej hovoríme jeden kyv. Doba jedného kyvu je polovičná oproti perióde, preto ju ďalej vo vzoráku budeme označovať ako \(T/2\).↩
Diskusia
Tu môžte voľne diskutovať o riešení, deliť sa o svoje kusy kódu a podobne.
Pre pridávanie komentárov sa musíš prihlásiť.