Zadanie
V jeden krásny slnečný deň sa Marek rozhodol ísť si zabehať. Ako tak bežal, vypadla mu jeho fľaša s vodou na zem — rovno do štrku. Bola to taká rana, že v nej ostalo niekoľko dier po kamienkoch. Marek si zarmútene zodvihol svoju obľúbenú fľašu a spozoroval, že z každej diery strieka voda inak. Zaujímalo by ho, čo to spôsobuje. Skúste mu to vysvetliť a ukázať - odmerajte závislosť dostreku vody vzhľadom na výšku dierky vo fľaši. Zistite, v akej výške sa nachádza dierka, z ktorej dostrekne voda najďalej.
Merajte iba s jednou dierou naraz a vždy používajte rovnaké množstvo vody vo fľaši. Meranie pre každú dierku vykonajte viackrát a určte strednú hodnotu a smerodajnú odchýlku. Namerané dáta vyneste do grafu a určte z nich optimálnu výšku. Nezabudnite sa vyjadriť k presnosti merania.
Majme fľašu s vodou, ktorej hladina je vo výške \(H\). Nech sú vo fľaši dierky v rôznej výške. Najskôr sa zamyslime nad tým, ako by mala vyzerať vzdialenosť dostreku \(d\) od výšky dierky \(z\) odo dna.
Čím je dierka hlbšie, tým je voda vystrekovaná pod vyšším tlakom, a teda vyššou rýchlosťou. Ak by bola dierka tesne pod hladinou, tak by voda pozvoľna vytekala, a teda by dostrekla do vzdialenosti presne \(\SI{0}{\metre}\). Na druhej strane, čím je hlbšie, tým je bližšie k podložke, na ktorú vyteká, a teda jej trvá kratšie, aby na ňu dopadla. V limitnom prípade, keď je dierka tesne pri dne, tak voda prakticky okamžite dopadne na podložku, čím je jej dostrek opäť \(\SI{0}{\metre}\). To znamená, že niekde medzi týmito dvomi limitnými polohami sa bude nachádzať maximum.
Môžeme si urobiť aj kvantitatívnu predpoveď. Uvažujme dierku vo výške \(z\) odo dna. Pre výtokovú rýchlosť platí Torricelliho vzorec \(v=\sqrt{2gh}\), kde \(h=H-z\) je výška hladiny nad dierkou.1 Voda vyteká z dierky vodorovne, čiže vykonáva vodorovný vrh, pre ktorého dĺžku platí \(d=v\sqrt{\frac{2z}{g}}\). Vylúčením výtokovej rýchlosti dostávame2 \[ d=2\sqrt{z\left(H-z\right)}\text{.} \]
Teraz už môžeme pristúpiť k meraniu. Namiesto fľaše použijeme nádobu valcového tvaru, pre ktorú sa bude jednoduchšie určovať dostrek, keďže všetky dierky budú presne nad sebou. Hladinu vody budeme mať vo výške \(H=\SI{20}{\centi\metre}\). Urobíme si tam značku, po ktorú budeme vodu vždy dopĺňať. Do nádoby si pripravíme dierky, pričom ich vzdialenosť volíme podľa toho, ako presne chceme výšku maximálneho dostreku určiť. My volíme dierky vo výškach \(z_{1}=\SI{5}{\centi\metre}\), \(z_{2}=\SI{7.5}{\centi\metre}\), \(z_{3}=\SI{10}{\centi\metre}\), \(z_{4}=\SI{12.5}{\centi\metre}\) a \(z_{5}=\SI{15}{\centi\metre}\). Všetky dierky prelepíme lepiacou páskou. Takto upravená nádoba je pripravená na meranie. Ešte si na podlahu umiestnime štvorčekový papier, ktorý nám zjednoduší odčítavanie dostreku.
Meranie bude prebiehať nasledovne. Vodu v nádobe doplníme po značku. Nádobu umiestnime na okraj štvorčekového papiera a jednu dierku odlepíme. Uvedomme si, že voda dostrekne najďalej v prvom momente, preto nemusíme čakať, kým všetka voda vytečie. Jednoducho si všimneme, kde voda dopadla v prvom momente a v tejto vzdialenosti si na papier položíme zápalku. Potom dierku opäť zalepíme a odčítame vzdialenosť zápalky od nádoby. Meranie opakujeme pre každú dierku päťkrát. Pred každým meraním podlahu dôkladne vyutierame a použijeme suchý štvorčekový papier.

Namerané dáta sú zapísané v tabuľke. Strednú hodnotu dostreku pre každú výšku vypočítame ako obyčajný aritmetický priemer. Smerodajnú odchýlku zase tak, že nájdeme, ako sa každá nameraná hodnota líši od priemernej hodnoty, vypočítame druhé mocniny týchto rozdielov a sčítame ich. Potom tento súčet predelíme počtom meraní krát počtom meraní mínus jedna a na záver z toho urobíme odmocninu. Matematicky zapísané \(\sigma=\sqrt{\frac{1}{n\cdot\left(n-1\right)}\sum_{i=1}^{n}\left(d_{i}-\overline{d}\right)^{2}}\), kde \(\overline{d}=\frac{1}{n}\sum_{i=1}^{n}d_{i}\) je spomínaná stredná hodnota dostreku.3 Ukážme si to na príklade výšky \(z_{3}=\SI{10}{\centi\metre}\). Stredná hodnota dostreku je \(\overline{d}=\frac{1}{5}\left(14+13+14.5+14+15\right)=\SI{14.1}{\centi\metre}\) a smerodajná odchýlka \(\sigma=\sqrt{\frac{1}{5\cdot4}\left[\left(14-14.1\right)^{2}+\left(13-14.1\right)^{2}+\left(14.5-14.1\right)^{2}+\left(14-14.1\right)^{2}+\left(15-14.1\right)^{2}\right]}\doteq\SI{0.33}{\centi\metre}\).
| Výška dierky \(z\) | \(\SI{15.0}{\centi\metre}\) | \(\SI{12.5}{\centi\metre}\) | \(\SI{10.0}{\centi\metre}\) | \(\SI{7.5}{\centi\metre}\) | \(\SI{5.0}{\centi\metre}\) |
|---|---|---|---|---|---|
| 1. meranie | \(\SI{6.5}{\centi\metre}\) | \(\SI{8.5}{\centi\metre}\) | \(\SI{14.0}{\centi\metre}\) | \(\SI{12.5}{\centi\metre}\) | \(\SI{11.5}{\centi\metre}\) |
| 2. meranie | \(\SI{6.0}{\centi\metre}\) | \(\SI{9.0}{\centi\metre}\) | \(\SI{13.0}{\centi\metre}\) | \(\SI{13.0}{\centi\metre}\) | \(\SI{10.0}{\centi\metre}\) |
| 3. meranie | \(\SI{7.0}{\centi\metre}\) | \(\SI{10.0}{\centi\metre}\) | \(\SI{14.5}{\centi\metre}\) | \(\SI{12.0}{\centi\metre}\) | \(\SI{10.5}{\centi\metre}\) |
| 4. meranie | \(\SI{5.5}{\centi\metre}\) | \(\SI{8.0}{\centi\metre}\) | \(\SI{14.0}{\centi\metre}\) | \(\SI{12.5}{\centi\metre}\) | \(\SI{12.0}{\centi\metre}\) |
| 5. meranie | \(\SI{6.0}{\centi\metre}\) | \(\SI{9.5}{\centi\metre}\) | \(\SI{15.0}{\centi\metre}\) | \(\SI{11.5}{\centi\metre}\) | \(\SI{11.5}{\centi\metre}\) |
| Stredná hodnota \(\overline{d}\) | \(\SI{6.2}{\centi\metre}\) | \(\SI{9.0}{\centi\metre}\) | \(\SI{14.1}{\centi\metre}\) | \(\SI{12.3}{\centi\metre}\) | \(\SI{11.1}{\centi\metre}\) |
| Smerodajná odchýlka \(\sigma\) | \(\SI{0.25}{\centi\metre}\) | \(\SI{0.35}{\centi\metre}\) | \(\SI{0.33}{\centi\metre}\) | \(\SI{0.25}{\centi\metre}\) | \(\SI{0.37}{\centi\metre}\) |
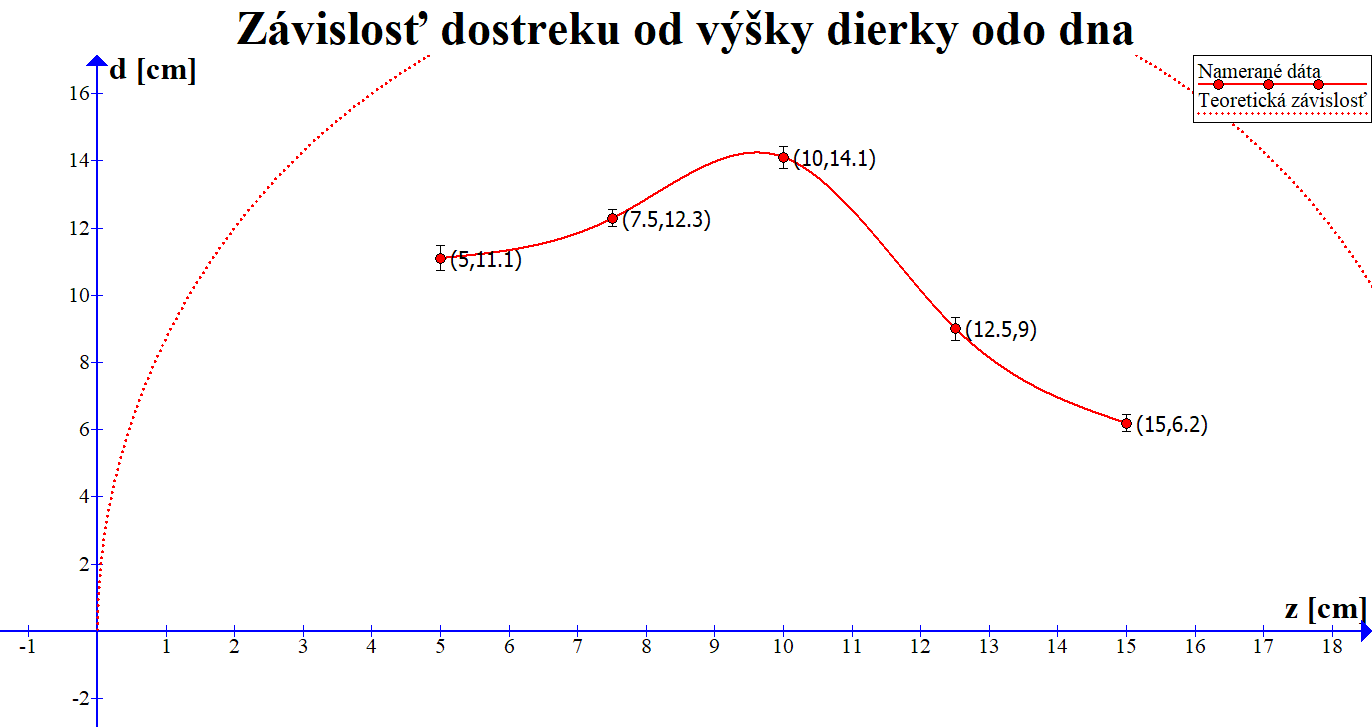
Na záver si vypočítané stredné hodnoty aj s príslušnými odchýlkami vykreslíme do grafu ako funkciu výšky dierky. Zobrazené body v grafe pospájame čiarou a z grafu odhadneme výšku dierky, pre ktorú je dostrek maximálny. Vidíme, že maximálnemu dostreku zodpovedá výška okolo \(z=\SI{10}{\centi\metre}\), čo zodpovedá našim očakávaniam. Už trochu menej zodpovedá našim očakávaniam veľkosť tohto maximálneho dostreku. Predpokladaný dostrek podľa teoretickej závislosti je totiž zobrazený na grafe bodkovanou čiarou a namerané hodnoty ležia výrazne nižšie. Je to spôsobené niekoľkými faktormi. V prvom rade sme zanedbali odpor vzduchu, takže skutočný dostrek je kratší než predpovedaný. Ďalej úlohu zohráva aj presný tvar a veľkosť dierok, ktoré určite neboli všetky úplne identické. Ďalej Torricelliho vzťah platí len približne – presne platí len vtedy, ak je dierka nekonečne malá, resp. hladina nekonečne veľká. Okrem toho úlohu mohlo zohrávať aj povrchové napätie, v dôsledku ktorého bola voda pri vytekaní mierne pribrzďovaná.
Komentár od opravovateľa
Všetky odovzdané riešenia mali jeden spoločný nedostatok – v úvode chýbal teoretický rozbor. Netreba sa toho vôbec báť. Obzvlášť ak je podobne ako v tomto prípade fyzika skúmaného javu pomerne jednoduchá.
Spísanie teórie je dôležitou súčasťou riešenia. V prvom rade si totiž treba ujasniť, čo idem merať. A rovnako to treba vysvetliť aj prípadnému čitateľovi vášho riešenia.
Okrem toho spracovanie teórie napomáha správnemu navrhnutiu experimentu. Konkrétne v tomto prípade nám dá predstavu o tom, kde sa hľadané maximum zhruba nachádza, a my vieme, že dierky do fľaše máme robiť hlavne v tejto oblasti. Na záver sa potom treba vrátiť k teórii, výsledky meraní s ňou porovnať a pokúsiť sa vysvetliť prípadné rozdiely.
Musím pochváliť Lukáša, ktorý ako jediný dostatočne teoreticky vysvetlil a matematicky popísal skúmaný jav. Aj keď treba priznať, že to tiež nebolo úplne ideálne, lebo tak urobil až po vykonaní experimentu, keď sa mu nepozdávali výsledky, ktoré dostával.
Dá sa to ľahko odvodiť zo zákona zachovania energie. Uvažujme malý kúsok kvapaliny s hmotnosťou \(m\). Ten má pri opúšťaní nádoby kinetickú energiu \(E_{k}=\frac{1}{2}mv^{2}\). Jeho miesto v nádobe zaberie kúsok kvapaliny, ktorý bol nad ním, miesto tohto kúska kúsok, ktorý bol nad ním, a tak ďalej. Efektívne tak ubudne kúsok z hladiny, a teda zmena potenciálnej energie bude \(E_{p}=-mgh\). Celková zmena energie má byť nulová, preto \(\frac{1}{2}mv^{2}=mgh\), odkiaľ \(v=\sqrt{2gh}.\)↩
Dá sa ukázať, že tento výraz dosahuje maximum pre \(z=\frac{H}{2}\). Vyžaduje si to ale použitie netriviálnej matematiky, preto to nebudeme robiť. Rovnako sa časom naučíte, že uvedená rovnica je rovnicou polkružnice, preto budeme očakávať, že namerané hodnoty na grafe vytvoria polkružnicu, odkiaľ je už zrejmé, že maximum by malo byť v polovičnej výške. Ale nepredbiehajme…↩
Výraz \(\sum_{i=1}^{n}x_{i}\) je ekvivalentný výrazu \(x_{1}+x_{2}+\dots+x_{n}\)↩
Diskusia
Tu môžte voľne diskutovať o riešení, deliť sa o svoje kusy kódu a podobne.
Pre pridávanie komentárov sa musíš prihlásiť.