3. Limonádová fontánka vzorové riešenie

V tejto úlohe ste mali za úlohu zmerať teplotnú objemovú rozťažnosť vody. Ak ste sa s týmto javom ešte vo fyzike nestretli¹, je to presne to, čo napovedá názov - teda to predstavuje, o koľko sa daný objem látky zväčší v závislosti od zmeny jeho teploty. Za domácu úlohu si môžete premyslieť, prečo sa pri zahrievaní látok bez zmeny skupenstva zväčšuje ich objem. Pri lineárnej objemovej rozťažnosti platí vzťah:

\[ \label{eq:(1)} V_1=V_0+\Delta V=V_0\,(1+\beta\Delta t)\text, \tag{1} \]

kde \(V_0\) je pôvodný objem látky (pred zahriatím), \(V_1\) je jej objem po zahriatí, \(\Delta t\) je zmena teploty a \(\beta\) je súčiniteľ teplotnej objemovej rozťažnosti. My sme od vás chceli, aby ste zmerali práve tento súčiniteľ. Z rovnice si preň vieme odvodiť vzorec \(\beta=\frac{V_1-V_0}{V_0\Delta t}=\frac{\Delta V}{V_0\Delta t}\), takže bolo potrebné zmerať len 3 veličiny, a to: pôvodný objem \(V_0\), zmenu teploty \(\Delta t\) (je už jedno, či v stupňoch Celzia alebo v Kelvinoch) a zmenu objemu \(\Delta V\).

Najprv si bolo potrebné vybrať vhodnú aparatúru. Keďže je zmena objemu \(\Delta V\) priamoúmerná pôvodnému objemu \(V_0\) a chceme mať čo najmenšiu odchýlku merania, bolo vhodné pri meraniach pracovať s čo najväčším objemom vody (ale len takým, aby ste ho boli schopní zahrievať rovnomerne) a tomu prispôsobiť výber nádoby. Na zahrievanie ste mohli použiť kahan, šporák, varič, kanvicu (vtedy by ste merali len samotné ochladzovanie), ale aj napríklad len sviečku.

Ďalšou podstatnou časťou bolo nájsť si vhodný spôsob odčítania zmeny objemu \(\Delta V\). Táto zmena sa dala merať aj napríklad hustomerom² (za predpokladu konštantnej hmotnosti), ale asi najbežnejším spôsobom bolo klasické odčítanie rozdielu výšky hladiny v nádobe. Ja osobne som preto použil ako nádobu varnú banku s úzkym hrdlom, aby som mohol čo najpresnejšie určovať zmenu výšky hladiny, ale stále môcť použiť relatívne veľký objem vody.

Pri samotnom meraní bolo dobré použiť dostatočne veľký rozdiel teplôt \(\Delta t\) (aspoň nejakých \(\SI{10}{\celsius}\)), ale zároveň čo najviac zabrániť strate vody odparovaním. Rovnako ako pri všetkých pokusoch, aj tu bolo dôležité kvôli presnosti výsledkov merania opakovať, merať na rôznych teplotných intervaloch, kvôli odstráneniu chýb spôsobených odparovaním vody merať najprv zväčšovanie a potom aj zmenšovanie objemu vody³ a samozrejme vyrátať aspoň nejakú odchýlku merania.

My sme merania opakovali (s každým postupom) 3 krát a odčítavali sme zmenu objemu približne po každých \(\SI{5}{\celsius}\), tu môžete vidieť graf závislosti zmeny objemu od zmeny teploty z jedného z meraní, pri ktorom sme vodu zahrievali.

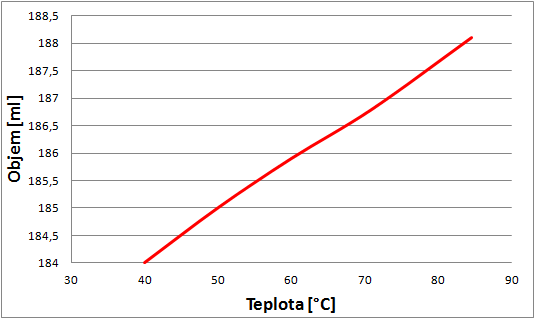
Výsledná nameraná hodnota závisela aj od použitej vody, vaše výsledky sa mali pohybovať okolo tabuľkovej hodnoty súčiniteľa teplotnej objemovej rozťažnosti vody \(\beta=\SI{2e-4}{\per\kelvin}\). Nám vyšla hodnota o niečo vyššia, naša priemerná nameraná hodnota bola približne \(\beta=\SI{3e-4}{\per\kelvin}\pm\SI{8e-5}{\per\kelvin}\).