5. Lúpež po slovensky vzorové riešenie

Pointa tohto javu nie je v ničom inom než vo fakte, že naša Zem sa otáča okolo svojej osi. Konkrétne Rím (a M&M, ktorý sa v Ríme nachádza) sa otáča väčšou rýchlosťou než Kodaň. Prečo je to tak?

Celá zemeguľa sa okolo osi otáčania pohybuje rovnakou uhlovou rýchlosťou – \(\ang{360}\) za deň. Toto platí aj pre všetky miesta na jej povrchu.

Každým miestom ale prechádza rovnobežka (kružnica) s iným polomerom a obvodom. Roviny, v ktorých sa tieto rovnobežky nachádzajú, sú kolmé na zemskú os. Všetky rovnobežky sú medzi sebou, naopak, rovnobežné. Najväčší z týchto kruhov je rovník, pri severnom či južnom póle sa kruhy zmenšujú.

Keďže každé miesto sa pohybuje tou istou uhlovou rýchlosťou, ale obvody kružníc sa líšia, líši sa aj skutočná obvodová rýchlosť pohybu týchto miest. Miesto na rovníku musí prekonať väčší obvod kružnice, aby sa za deň otočilo okolo osi o \(360\) stupňov, teda sa pohybuje rýchlejšie. Naopak, severný a južný pól pretína os otáčania, teda tieto miesta sa za celý deň vplyvom otáčania Zeme pohnú len minimálne („vôbec“).

\(v_R = \frac{\num{2}\pi \cdot \SI{6371}{\kilo\metre} }{\SI{24}{\hour}} = \SI{463.3}{\metre\per\second}\) je rýchlosť otáčania na rovníku. Vypočítali sme ju ako obvod rovníka delený počtom sekúnd v dni.

Nás ale zaujíma, akou rýchlosťou sa hýbe Rím po svojej geografickej rovnobežke. Treba zistiť, aký je jej obvod. To zistíme tak, že spočítame jej polomer.

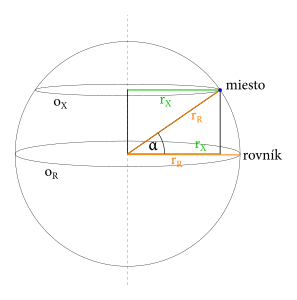
V geometrickom obraze celej situácie nájdeme pravouhlý trojuholník, ktorého prepona je rovná polomeru Zeme (čo je aj polomer rovníka – najväčšej rovnobežky – na obrázku \(r_R\)), a ktorého odvesna je rovná hľadanému polomeru \(r_X\). Zistíme, že uhol vyjadrujúci geografickú šírku (ak ste náhodou zabudli, geografická šírka sa vyjadruje práve v uhle) je uhol pri odvesne \(r_X\). Preto vieme vyjadriť \(r_X\) ako \(r_R \cos(\alpha)\), kde \(\alpha\) je geografická šírka.

Keď vidíme, že polomer v danom mieste sa rovná \(r_R \cdot \cos(\alpha)\), vieme si odvodiť, že obvod danej rovnobežky sa bude rovnať \(o_R \cdot \cos(\alpha)\). Keďže rýchlosť, ktorou sa daný bod musí otáčať, je zase priamo úmerná k obvodu, rýchlosť otáčania v danom bode sa rovná \(v_R \cdot \cos(\alpha)\).

Rýchlosť otáčania v Ríme je teda \(v_R \cdot \cos(\ang{41.9}) = \SI{344.8}{\metre\per\second}\) a v Kodani \(v_R \cdot \cos(\ang{55.67}) = \SI{261.2}{\metre\per\second}\).

M&M sa teda teleportuje do Kodane pohybujúc sa v kruhovom pohybe okolo zemskej osi rýchlosťou o \(\SI{83.6}{\metre\per\second}\) väčšou než samotná Kodaň, čo má za následok jeho náraz do najbližšej steny v smere otáčania Zeme. V kilometroch za hodinu je to rýchlosťou \(\SI{302}{\kilo\metre\per\hour}\).

To nie je ešte úplne všetko: Rím a Kodaň majú skoro rovnakú geografickú dĺžku, takže tento druhý efekt nie je badateľný, ale ak by sme mali dve mestá, ktoré sa aj v tejto súradnici výrazne líšia, museli by sme zarátať aj to, že vektor rýchlosti, ktorý je v jednom meste kolmý na povrch Zeme, by v druhom smeroval do podlahy alebo do stropu. M&M by okrem pohybu smerom k stene zažil aj pohyb nahor (prípadný náraz do stropu) alebo nadol (náraz do podlahy).¹