Zadanie
Na teleso pohybujúce sa v odporovom prostredí pôsobí odporová sila prostredia. Jej veľkosť je daná Newtonovým odporovým vzťahom1 \(F=\frac{1}{2}CS\rho v^2\), kde \(C\) je koeficient zohľadňujúci tvar telesa, \(S\) je čelný prierez, čiže veľkosť plochy, ktorú vidíme, keď sa na teleso pozeráme spredu, \(\rho\) je hustota prostredia a \(v\) je rýchlosť, ktorou sa teleso hýbe. Odporová sila vždy pôsobí proti smeru pohybu.
Kvalitatívne popíšte, ako vyzerá pád v odporovom prostredí. Ako sa mení rýchlosť padajúcej loptičky v odporovom prostredí s časom?
Krtko si zohnal veľmi vysokú vákuovú komoru, aby odhalil vplyv odporu vzduchu na pád loptičky. Postupne spúšťal loptičku z čoraz väčšej výšky – jednak v bežnej atmosfére, a potom aj vo vákuovej komore – a meral doby pádov. Výsledky oboch experimentov zaznačil do grafu. Pokúste sa nakresliť, ako vyzeral Krtkov graf. Zamyslite sa a odhadnite, akou rýchlosťou dopadala na zem Krtkova loptička padajúca v atmosfére za predpokladu, že ju hádzal z dostatočne veľkej výšky. Následne si svoje odhady overte simulovaným experimentom. Nezabúdajte uvádzať hodnoty všetkých parametrov, ktoré ste použili v simulácii.
Potom Krtko našiel poklad – truhlicu s loptičkami identickej veľkosti. Každá však bola z iného materiálu, a teda mali odlišné hmotnosti. To Krtko nemohol nevyužiť a začal ich postupne spúšťať z tej istej výšky na zem, pričom meral dobu pádu. Namerané dáta zakresľoval do grafu závislosti doby pádu od hmotnosti loptičky.
Najskôr sa zamyslite, ako Krtkov graf vyzeral. Prečo by mal vyzerať práve tak? Potom odsimulujte experiment a overte si svoju hypotézu.
Newtonov odporový vzťahpoužívame pri turbulentnom prúdení, t. j. vtedy, keď za telesom vznikajú víry. Ak víry nevznikajú, vtedy hovoríme o laminárnom prúdení a používame tzv. Stokesov vzťah.↩︎
Teoretický úvod
V prvej úlohe sme si povedali, že počas voľného pádu (v bezodporovom prostredí) objekt zväčšuje svoju rýchlosť každú sekundu o \(\SI{9.81}{\metre\per\second}\), a to až dovtedy, dokým nedopadne. Čo by sa stalo, ak by sme oproti gravitačnej sile postavili (do presne opačného smeru) nejakú silu \(F_{\mathrm{op}}\), najskôr uvažujúc, že má nemennú veľkosť?
Ak je \(F_{\mathrm{op}}\) menšia než gravitačná sila, teleso bude stále zrýchľovať smerom nadol, aj keď menším tempom. Ak je \(F_{\mathrm{op}}\) rovnaká, teleso nebude meniť svoju rýchlosť – tieto dve sily sa navzájom celkom vyrušia. Ak by \(F_{\mathrm{op}}\) bola väčšia, teleso začne zrýchľovať v opačnom smere, než ako pôsobí gravitačná sila.
Naša odporová sila je takouto opačnou silou, ale my vieme, že jej veľkosť nie je konštantná, ale závisí priamo úmerne na rýchlosti telesa – dokonca kvadraticky. Ostatné faktory, ktoré na ňu vplývajú, sa v priebehu pádu nemenia – ide o prierez loptičky, jej aerodynamický koeficient a hustotu prostredia.
Podľa vzorca vidíme, že odporová sila je na začiatku pádu nulová. Potom sa zväčšuje priamo úmerne s rýchlosťou. Pokiaľ je menšia, než rýchlosť, platí prvá spomenutá situácia – loptička stále zrýchľuje, len čoraz pomalším tempom, lebo odporová sila sa zväčšuje. Čo sa stane, keď sa odporová sila vyrovná gravitačnej? Nastane druhá situácia. Loptička celkom prestane zrýchľovať. A v takom stave už ostane – rýchlosť sa nemení, čiže ani odporová sila sa nemení, ostáva rovná gravitačnej. A rýchlosť, ktorú sme dosiahli, sa nazýva terminálna (konečná) rýchlosť – ktorou už bude teleso padať po celý zvyšok svojho pádu.
Terminálnu rýchlosť vieme zistiť tak, že dáme do rovnosti odporovú a gravitačnú silu, následne vyjadríme. \[F_O = F_G\] \[\frac{CS\rho v^2}{\num{2}} = mg\] \[v^2 = \frac{\num{2}mg}{CS\rho}\] \[v = \sqrt{\frac{\num{2}mg}{CS\rho}}\]
Doba pádu v závislosti od výšky nad Zemou
Zamyslenie:
Čas dosiahnutia terminálnej rýchlosti je pre rovnaké teleso vo voľnom páde vždy rovnaký, bez ohľadu na to, či ho púšťam z väčšej výšky, keďže výška neovplyvňuje odporovú silu a nijako badateľne neovplyvňuje ani gravitačnú silu1. Každý voľný pád v odporovom prostredí tak vieme rozdeliť na dve časti – pred dosiahnutím terminálnej rýchlosti, a ak padalo teleso dostatočne dlho aby ju dosiahlo, aj na časť po dosiahnutí terminálnej rýchlosti.
Čo sa týka časti pred dosiahnutím terminálnej rýchlosti, všimnime si, že čím bližšie k tejto rýchlosti sme, tým menšia je akcelerácia – tým pomalšie rýchlosť rastie. Ale stále rastie, takže keď pridáme ďalší meter k existujúcej dĺžke pádu, prejdeme ho priemerne za menej.
Čo sa týka časti po dosiahnutí terminálnej rýchlosti, ak budeme pridávať ďalšiu dráhu, po nej už bude loptička padať terminálnou rýchlosťou. Tá je konštantná, teda prírastok času bude odtiaľto rásť lineárne – v grafe uvidíme od tohto času priamku pod nejakým konkrétnym sklonom.
Meranie:
Simuláciu sme vykonali s objektom, pri ktorom bude najlepšie vidieť rozdiel medzi pádom vo vzdušnej atmosfére a pádom vo vákuu – plážovou loptou. Plážová lopta môže mať polomer okolo \(\SI{15}{\centi\metre}\) a odhadli sme, že váži približne \(\SI{25}{\gram}\). Najprv sme simulovali jej pád v odporovom prostredí:
| Výška | Doba pádu |
|---|---|
| \(\num{0}\) | \(\num{0}\) |
| \(\num{5}\) | \(\num{2.95}\) |
| \(\num{10}\) | \(\num{5.47}\) |
| \(\num{15}\) | \(\num{7.98}\) |
| \(\num{20}\) | \(\num{10.50}\) |
| \(\num{25}\) | \(\num{13.00}\) |
| \(\num{30}\) | \(\num{15.53}\) |
| \(\num{35}\) | \(\num{18.04}\) |
| \(\num{40}\) | \(\num{20.56}\) |
| \(\num{45}\) | \(\num{23.07}\) |
| \(\num{50}\) | \(\num{25.59}\) |
| \(\num{55}\) | \(\num{28.10}\) |
| \(\num{60}\) | \(\num{30.62}\) |
| \(\num{65}\) | \(\num{33.13}\) |
| \(\num{70}\) | \(\num{35.65}\) |
| \(\num{75}\) | \(\num{38.16}\) |
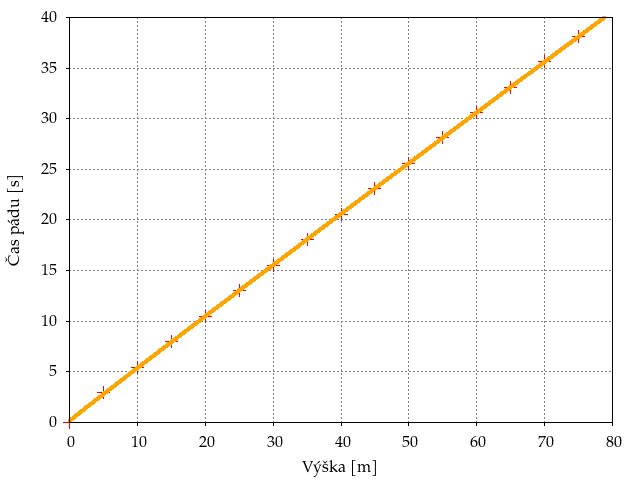
A potom vo vákuu:
| Výška | Doba pádu |
|---|---|
| \(\num{0}\) | \(\num{0}\) |
| \(\num{5}\) | \(\num{1.01}\) |
| \(\num{10}\) | \(\num{1.43}\) |
| \(\num{15}\) | \(\num{1.75}\) |
| \(\num{20}\) | \(\num{2.02}\) |
| \(\num{25}\) | \(\num{2.26}\) |
| \(\num{30}\) | \(\num{2.48}\) |
| \(\num{35}\) | \(\num{2.67}\) |
| \(\num{40}\) | \(\num{2.86}\) |
| \(\num{45}\) | \(\num{3.03}\) |
| \(\num{50}\) | \(\num{3.20}\) |
| \(\num{55}\) | \(\num{3.35}\) |
| \(\num{60}\) | \(\num{3.50}\) |
| \(\num{65}\) | \(\num{3.64}\) |
| \(\num{70}\) | \(\num{3.78}\) |
| \(\num{75}\) | \(\num{3.91}\) |
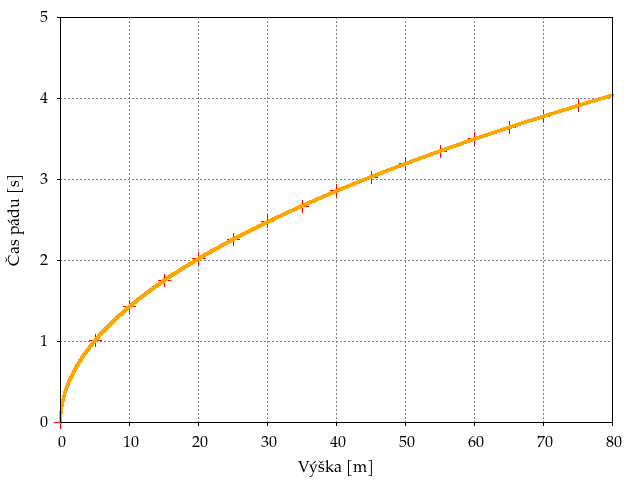
Simulácia nám potvrdila náš predpoklad – pri páde v atmosfére sme veľmi rýchlo dosiahli terminálnu rýchlosť (ktorá bola malá, teda pád trval dlho) a ďalej sa čas pádu zvyšoval lineárne v závislosti od pridanej výšky. Pri páde vo vákuu sa zase teleso správalo tak, ako sme odvodili v úlohe 1, doba pádu bola nezávislá od hmotnosti a tvaru, bola závislá iba od počiatočnej výšky, a to odmocninovo.
Doba pádu v závislosti od hmotnosti
Zamyslenie:
Ak máme rovnako veľkú loptičku, vzťah pre odporovú silu vyjde rovnaký bez ohľadu na hmotnosť. Avšak gravitačná sila je závislá od hmotnosti. V ľubovoľnom okamihu pádu teda ostane po odčítaní odporovej sily viac gravitačnej sily pri ťažšej loptičke než pri ľahšej. Zrýchlenie v danom okamihu bude teda väčšie. Celkový predpoklad by teda bol, že hustejšia loptička bude menej ovplyvnená odporom vzduchu.
Meranie:
Simuláciu sme vykonali s loptičkami o polomere \(\SI{5}{\centi\metre}\) a o hmotnosti postupne \(\SIlist[quotient-mode = fraction, list-final-separator = \text{ a }, fraction-function = \dfrac] {1;1/2;1/4;1/8;1/16;1/32;1/64}{\kilo\gram}\). Púšťali sme ich z výšky \(\SI{75}{\metre}\).
| Hmotnosť | Doba pádu |
|---|---|
| \(\num{0.01563}\) | \(\num{9.81}\) |
| \(\num{0.03125}\) | \(\num{7.28}\) |
| \(\num{0.0625}\) | \(\num{5.71}\) |
| \(\num{0.125}\) | \(\num{4.82}\) |
| \(\num{0.25}\) | \(\num{4.36}\) |
| \(\num{0.5}\) | \(\num{4.14}\) |
| \(\num{1}\) | \(\num{4.02}\) |
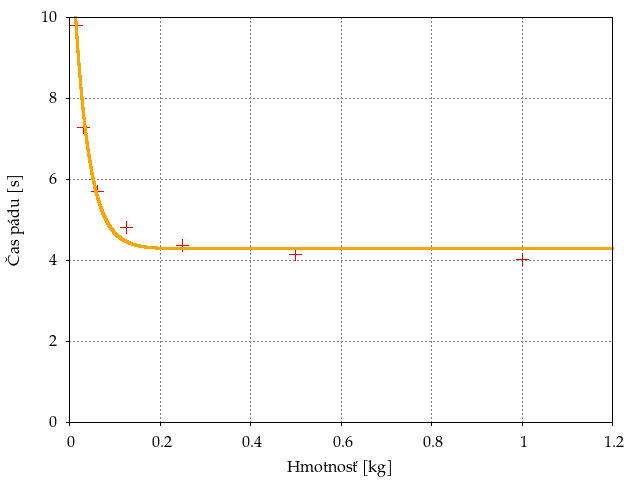
Je to pomerne výpovedné – medzi loptičkou o hmotnosti \(\SI{1}{\kilo\gram}\) a loptičkou o hmotnosti \(\SI[quotient-mode = fraction, fraction-function = \dfrac]{1/64}{\kilo\gram}\) pozorujeme viac ako dvojnásobný nárast v čase pádu spôsobený odporom vzduchu.
Pokiaľ našu loptičku nepúšťame niekde z horného okraja atmosféry.↩︎
Diskusia
Tu môžte voľne diskutovať o riešení, deliť sa o svoje kusy kódu a podobne.
Pre pridávanie komentárov sa musíš prihlásiť.